Tabellen und Formeln
SI-Basiseinheiten
Größe | SI-Einheit | Symbol |
|---|---|---|
Länge | Meter | m |
Masse | Kilogramm | kg |
Zeit | Sekunde | s |
Elektrische Stromstärke | Ampere | A |
Temperatur | Kelvin | K |
Lichtstärke | Candela | cd |
Stoffmenge | Mol | mol |
Physikalische Konstanten
Bezeichnung | Kurzzeichen | Wert |
|---|---|---|
Fallbeschleunigung | g | 9,81m⋅s−2 |
Lichtgeschwindigkeit im Vakuum | c | 2,998⋅108m⋅s−1 |
Avogadro-Konstante | NA | 6,022⋅1023mol−1 |
Molvolumen idealer Gase (bei 273,15K und 101,325kPa) |
| 22,4l⋅mol−1 |
Dichte von Wasser (bei 20°C) |
| 0,998⋅103kg⋅m−3 |
Dichte von Luft (bei 273,15K und 101,325kPa) |
| 1,29kg⋅m−3 |
Gaskonstante, molare | R | 8,314J⋅mol−1⋅K−1 |
Erdradius am Äquator |
| 6378km |
Masse der Erde |
| 5,98⋅1024kg |
Mittlerer Abstand Erde-Sonne |
| 1,496⋅108km |
Atomare Masseneinheit | u | 1,66⋅10−27kg |
Ruhemasse des Elektrons | me | 9,11⋅10−31kg |
Ruhemasse des Protons | mp | 1,67⋅10−27kg |
Elementarladung | e | 1,6⋅10−19C |
Vielfache und Teile von Einheiten
Zehnerpotenz | Vorsatz | Kurzbezeichnung |
|---|---|---|
1018 | Exa | E |
1015 | Peta | P |
1012 | Tera | T |
109 | Giga | G |
106 | Mega | M |
103 | Kilo | k |
102 | Hekto | h |
101 | Deka | da |
100 |
|
|
10−1 | Dezi | d |
10−2 | Centi | c |
10−3 | Milli | m |
10−6 | Mikro | μ |
10−9 | Nano | n |
10−12 | Pico | p |
10−15 | Femto | f |
10−18 | Atto | a |
Geometrie
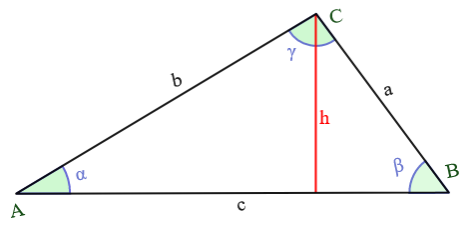
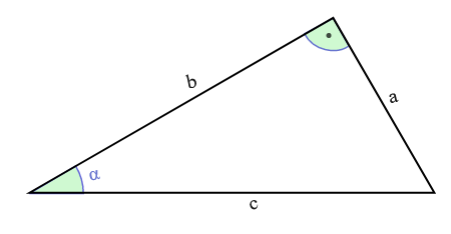
Dreieck
Allgemein:
$ \alpha + \beta + \gamma = 180° $
$ A = \frac{1}{2} \cdot c \cdot h = \frac{1}{2} \cdot b \cdot c \cdot sin \alpha $
$ U = a + b + c $
Rechtwinkliges Dreieck:
$ \gamma = 90° $ und $ \alpha + \beta = 90° $
$ A = \frac{1}{2} \cdot a \cdot b $
$a^2 + b^2 =c^2$
Zum rechtwinkligen Dreieck s. auch Trigonometrie
Schaubild von Thomas Steiner, CC BY-SA 3.0, Link
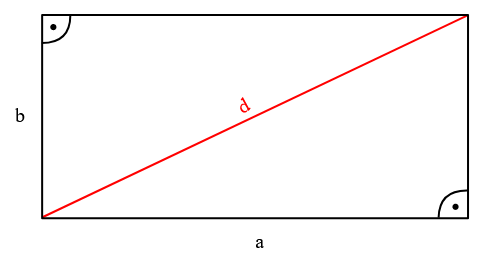
Rechteck
Allgemein:
$A=a \cdot b$
$U=2 \cdot a + 2 \cdot b$
$d=\sqrt{a^2 + b^2}$
Quadrat: a = b
$A=a^2$
$U=4 \cdot a$
$d=a \cdot \sqrt{2}$
Schaubild von XZise - Eigenes Werk, CC BY-SA 3.0, Link
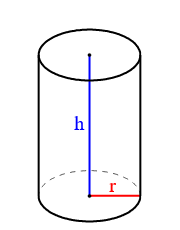
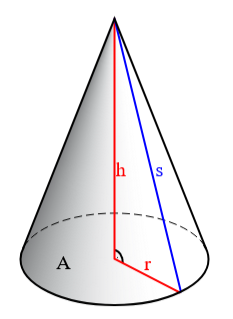
Zylinder
Ein Zylinder ist eine Säule mit kreisförmiger Grundfläche.
$V = A \cdot h = \pi \cdot r^2 \cdot h$
$O=M+2 \cdot A = 2 \cdot \pi \cdot r \cdot h+2 \cdot \pi \cdot r^2=2 \cdot \pi \cdot r \cdot (h+r)$
Schaubild von Ag2gaeh - Eigenes Werk, CC-BY-SA 4.0, Link
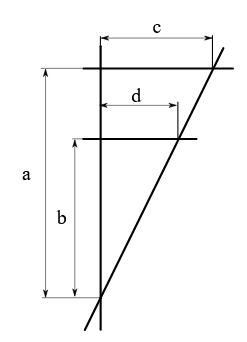
Strahlensatz
Wenn zwei Geraden ('Strahlen') durch einen Punkt verlaufen und von zwei parallelen Geraden geschnitten werden, dann entstehen zwei ähnliche Dreiecke. Die korrespondierenden Seiten der Dreiecke stehen im selben Verhältnis zueinander, z. B.:
$\frac{a}{b} = \frac{c}{d}$
Schaubild von Petrus3743 - Eigenes Werk, CC-BY-SA 4.0, Link
Trigonometrie
Winkelfunktionen
Zu Winkelfunktionen s. auch Funktionen
Im rechtwinkligen Dreieck sind die bekanntesten Winkelfunktionen für spitze Winkel als Verhältnis zweier Seiten definiert:
$\sin \alpha = \frac{Gegenkathete}{Hypothenuse}=\frac{a}{c}$
$\cos \alpha = \frac{Ankathete}{Hpothenuse}= \frac{b}{c}$
$\tan \alpha = \frac {Gegenkathete}{Ankathete} =\frac {a}{b} $
Die Hypotenuse ist die Seite, die dem rechten Winkel gegenüberliegt. Die Katheten sind die Seiten, die den rechten Winkel einschließen. Die Ankathete ist die Seite, die an den jeweils betrachteten Winkel grenzt.
Arcusfunktionen
Wenn Sie den Wert einer Winkelfunktion kennen, dann können Sie mit der Arkusfunktion den zugehörigen Winkel bestimmen, z. B.:
$\sin \alpha = 0,5 \Rightarrow \alpha = \arcsin(0,5) = 30°$
Manche Taschenrechner haben für die Umkehrfunktionen allgemein eine 'INV'-Taste, z. B. ist arcsinx durch die beiden Tasten 'INV SIN' realisiert. Achtung: Die Arkusfunktionen sind mehrdeutig. Außerdem müssen Sie beachten, ob Ihr Taschenrechner das Resultat im Grad- oder Bogenmaß ausgibt!
Winkelfunktion | zugehörige Arkusfunktion |
|---|---|
$\sin x$ | $\arcsin x$ oder $\sin^{−1} x$ |
$\cos x$ | $\arccos x$ oder $\cos^{−1} x$ |
$\tan x$ | $\arctan x$ oder $\tan^{−1} x$ |
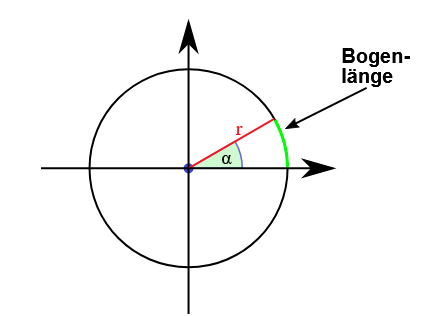
Winkelmaße
Im Gradmaß wird der Vollwinkel ('einmal ganz herum') in 360 gleiche Teile zerlegt, die Winkelgrade. Zum Beispiel hat ein 'rechter Winkel' dann 90°.
Im Bogenmaß wird ein Winkel als Quotient aus der Bogenlänge eines Kreises und dem zugehörigen Radius definiert. Der Vollwinkel hat den Wert $2\pi$. Häufig wird die Einheit 'rad' (Radian) hinzugefügt.
Umrechnung:
$\alpha_{rad} = \frac{\pi}{180°} \cdot \alpha_{Grad}$
$\alpha_{Grad} = \frac{180°}{\pi} \cdot \alpha_{rad}$
Beziehungen zwischen den Winkelfunktionen
Einige häufig benutzte Relationen sind:
$\cos x = \sin (x+\frac{\pi}{2})$ und $\sin x = \cos (x-\frac{\pi}{2})$
$\sin^2 x + \cos^2 x = 1$
$\tan x =\frac{\sin x}{\cos x}=\frac{1}{\cot x}$
$\sin(\alpha \pm \beta) = \sin \alpha \cdot \cos \beta \pm \sin \alpha \cdot \sin \beta$
$\cos(\alpha \pm \beta) = \cos \alpha \cdot \cos \beta \mp \sin \alpha \cdot \sin \beta$
Algebra
Rechnen mit Potenzen und Wurzeln
$a^m \cdot a^n = a^{m+n}$
$a^n \cdot b^n = (a \cdot b)^n$
$(a^m)^n = a^{m \cdot n} = (a^n)^m$
$a^1=a$
$\sqrt[n]{a} \cdot \sqrt[n]{b}=\sqrt[n]{a \cdot b}$
$(\sqrt[n]{a})^m=\sqrt[n]{a^m}$
$a^{-n}=\frac{1}{a^n}$
$\frac{a^m}{a^n}= a^{m-n}$
$\frac{a^n}{b^n}= (\frac{a}{b})^n$
$a^{\frac{m}{n}} = \sqrt[n]{a^m}$
$a^0=1$ (für a $\neq$ 0)
$\frac{\sqrt[n]{a}}{\sqrt[n]{b}}= \sqrt[n]{\frac{a}{b}}$
$\sqrt[m]{\sqrt[n]{a}}=\sqrt[m \cdot n]{a}=\sqrt[n]{\sqrt[m]{a}}$
Rechnen mit Logarithmen
$\log_a b$ ist die Zahl, mit der man $a$ (die 'Basis') potenzieren muss, um $b$ zu erhalten:
$b=a^x \Leftrightarrow \log_a b = x \Rightarrow b=a^{\log_a b}$
$a:=10 \Rightarrow \log_{10} b = \lg b$
$a:=e \Rightarrow \log_e b = \ln b$
$\log_a b = \frac{\log_c b}{\log_c a}$
$\ln r = 2,3026 \cdot \lg r$
$\lg r =0,4343 \cdot \ln r$
$\log_a (u \cdot v) = \log_a u + \log_a v$
$\log_a (\frac{u}{v}) = \log_a u - \log_a v$
$\log_a u^m = m \cdot \log_a u$
$\log_a \sqrt[n]{u} = \log_a u^{\frac{1}{n}} = \frac{1}{n}\log_a u$
$\log_a (\frac{1}{v}) = \log_a 1 - \log_a v = 0 - \log_a v = -\log_a v$
Quadratische Gleichungen
Die allgemeine quadratische Gleichung können Sie in die 'Normalform' umformen. Es gibt zwei (unter Umständen komplexe) Lösungen für $x$.
$a \cdot x^2+b \cdot x+c=0$ |:$a \qquad \Rightarrow x^2+p \cdot x+q=0$
mit $p = \frac{b}{a}$ und $q = \frac{c}{a}\Rightarrow x_{1,2}=-\frac{p}{2} \pm \sqrt{(\frac{p}{2})^2-q}$ bzw. $x_{1,2}=\frac{-b \pm \sqrt{b^2 - 4 \cdot a \cdot c}}{2 \cdot a}$
Näherungen
Für 'kleine Werte von x' können Sie die folgenden Näherungen benutzen. Die Genauigkeit der Näherung ist berechenbar, s. Mathematikvorlesung!
$(1 \pm a)^n \approx 1 \pm n \cdot x $
$e^{\pm x} \approx 1 \pm x $
$\frac{1}{1+x} \approx 1 - x $
$a^x \approx 1 + \ln (a) \cdot x $
$\sqrt{1 + x} \approx 1 + \frac{1}{2}x $
$\ln (1 \pm x) \approx \pm x $
$\frac{1}{\sqrt{1+x}} \approx 1 -1 \frac{1}{2}x$
$\sin x \approx x$ und $\tan x \approx x$
$\cos x \approx 1 - \frac{1}{2}x^2$
Vektoren
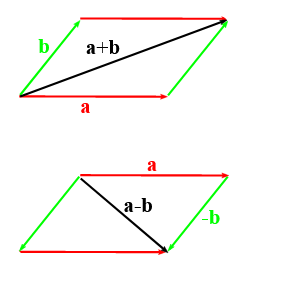
Vektoraddition
$\textbf{a} = \begin{pmatrix} a_x \\ a_y \\ a_z \end{pmatrix}$ $\textbf{b} = \begin{pmatrix} b_x \\ b_y \\ b_z \end{pmatrix}$ $\textbf{a}+\textbf{b} = \begin{pmatrix} a_x + b_x\\ a_y + b_y\\ a_z + b_z \end{pmatrix}$
$-\textbf{b} = \begin{pmatrix} -b_x \\ -b_y \\ -b_z\end{pmatrix}$ $\textbf{a}-\textbf{b} = \begin{pmatrix} a_x - b_x\\ a_y - b_y\\ a_z - b_z \end{pmatrix}$
$\textbf{a}+\textbf{b}=\textbf{b}+\textbf{a}$
$\textbf{a}-\textbf{b}=\textbf{a}+(-\textbf{b})$
Betrag eines Vektors
$\textbf{a} = \begin{pmatrix} a_x \\ a_y \\ a_z \end{pmatrix}$ $|\textbf{a}| = \sqrt{a^2_x + a^2_y + a^2_z}$
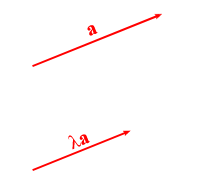
Die Multiplikation eines Vektors $\textbf{a}$ mit einer positiven Zahl $\lambda$ führt zu einem Vektor mit derselben Richtung wie $\textbf{a}$, aber der Länge $\lambda \textbf{a}$. Ist die Zahl $\lambda$ negativ, ist $\lambda \textbf{a}$ dem Vektor $\textbf{a}$ entgegengerichtet.
$\lambda \textbf{a} = \begin{pmatrix} a_x \\ a_y \\ a_z \end{pmatrix}$ $|\lambda \textbf{a}| = |\lambda| \cdot |\textbf{a}|$
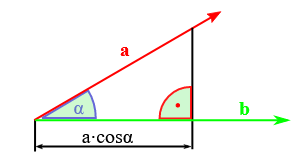
Skalarprodukt
$\textbf{a} = \begin{pmatrix} a_x \\ a_y \\ a_z \end{pmatrix}$ $\textbf{b} = \begin{pmatrix} b_x \\ b_y \\ b_z \end{pmatrix}$
$\textbf{a} \cdot \textbf{b} = a_x b_x + a_y b_y + a_z b_z = |\textbf{a}| \cdot |\textbf{b}| \cdot \cos{\alpha}$
$\textbf{a} \cdot \textbf{b} = \textbf{b} \cdot \textbf{a}$
$\textbf{a} \cdot \textbf{b} = 0 \Leftrightarrow \textbf{a} \bot \textbf{b}$ oder $\textbf{a}=0$ oder $\textbf{b}=0$
$\textbf{a} \cdot \textbf{a} = |\textbf{a}|^2 = a^2 = a^2_x + a^2_y + a^2_z$
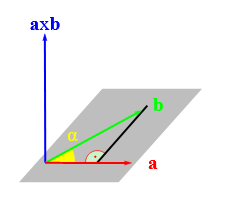
Kreuzprodukt
Das Kreuzprodukt $\textbf{a} \times \textbf{b}$ steht senkrecht auf $\textbf{a}$ und senkrecht auf $\textbf{b}$, also senkrecht auf der von $\textbf{a}$ und $\textbf{b}$ aufgespannten Ebene.
$\textbf{a} = \begin{pmatrix} a_x \\ a_y \\ a_z \end{pmatrix}$ $\textbf{b} = \begin{pmatrix} b_x \\ b_y \\ b_z \end{pmatrix}$ $\textbf{a} \times \textbf{b} = \begin{pmatrix} a_yb_z - a_zb_y\\ a_zb_x - a_xb_z\\ a_xb_y - a_yb_x \end{pmatrix}$
$|\textbf{a} \times \textbf{b}|= |\textbf{a}| \cdot |\textbf{b}| \cdot \sin{\alpha}$
$\textbf{a} \times \textbf{b} = -\textbf{b} \times \textbf{a}$
$\textbf{a} \times \textbf{b} = 0 \Leftrightarrow \textbf{a} || \textbf{b}$ oder $\textbf{a}=0$ oder $\textbf{b}=0$
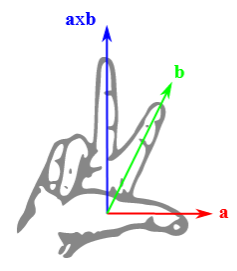
Kreuzprodukt - 'Rechte-Hand-Regel'
Die Vektoren $\textbf{a},\textbf{b}$ und ihr Kreuzprodukt $\textbf{a} \times \textbf{b}$ bilden ein Rechtssystem. Die Orientierung von $\textbf{a} \times \textbf{b}$ relativ zu $\textbf{a}$ und $\textbf{b}$ kann man sich z. B. anhand der 'Rechte-Hand-Regel' merken:
Wenn der Daumen in Richtung von $\textbf{a}$ und der Zeigefinger in Richtung von $\textbf{b}$ deutet, hat der senkrecht dazu stehende Mittelfinger der rechten Hand die Richtung von $\textbf{a} \times \textbf{b}$.
Achtung Linkshänder: Diese Merkregel funktioniert nur mit der rechten Hand. Wenn Sie die linke Hand benutzen, bekommen Sie einen entgegengesetzt gerichteten Vektor!
Koordinatensysteme
Kartesisches Koordinaten
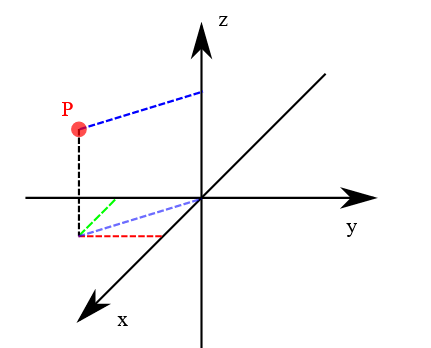
Das kartesische Koordinatensystem besteht aus drei zueinander senkrecht stehenden Koordinatenachsen x, y und z. Sie schneiden sich in einem Punkt, dem Ursprung oder Nullpunkt des Systems. Koordinaten, die vom Nullpunkt aus in Richtung der 'Pfeilspitze' der Achse liegen, sind positiv, in Gegenrichtung negativ.
Ein Punkt P im Raum wird durch die drei Koordinaten x, y, z bezeichnet. Sie geben die Lage der senkrechten Projektion des Punktes P auf die jeweilige Achse an.