Angewandte Mathematik (Master)
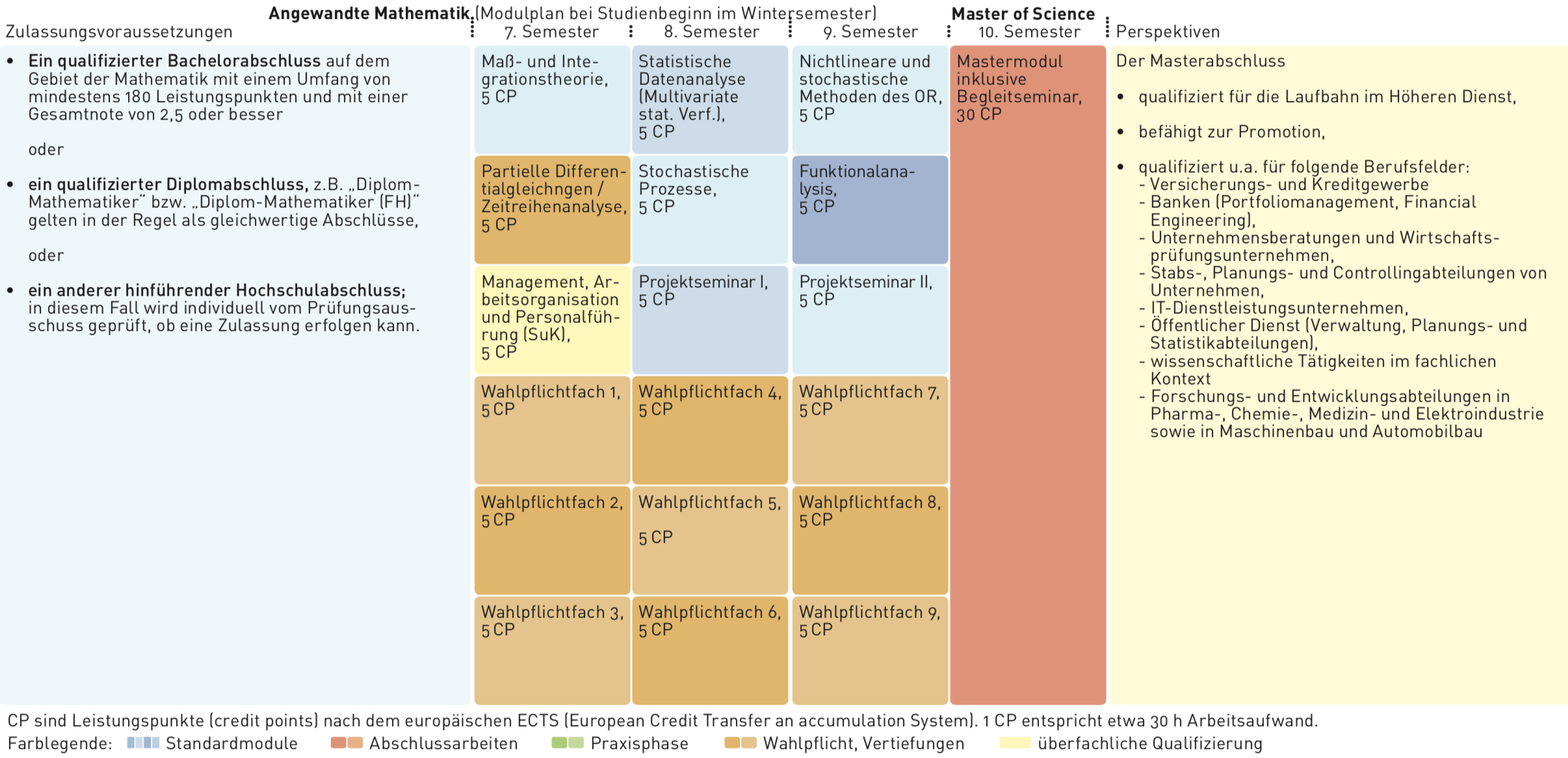
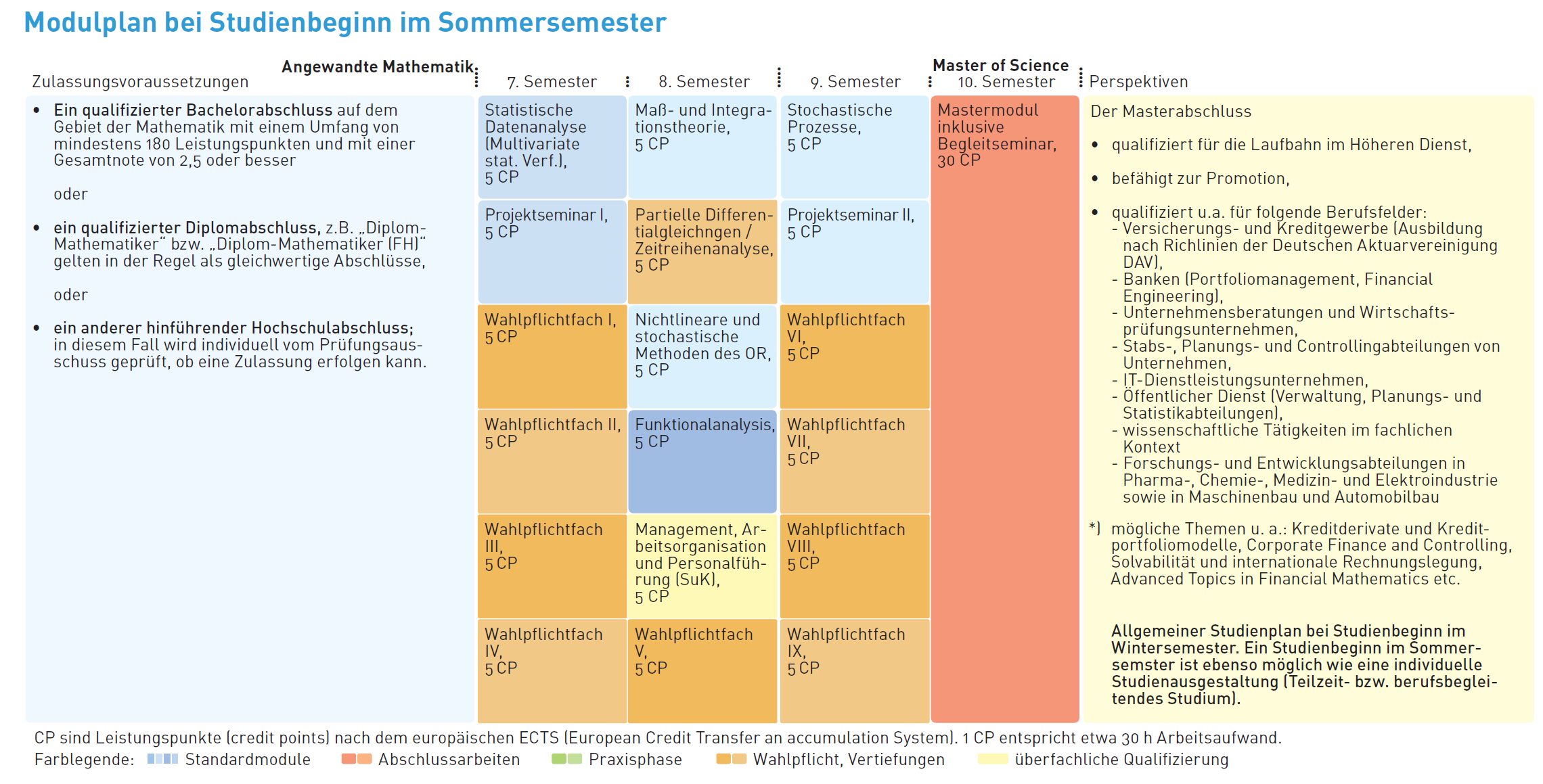
Gegenstand des 4-semestrigen Masterstudiums Angewandte Mathematik (M. Sc.) sind die modernen Anwendungsfelder der Mathematik im Bereich Finanzen, Versicherungen, Operations Research und Stochastik sowie Technomathematik. Die wichtigstens Informationen sind im Studiengangsflyer zusammengestellt.
Bezeichnung | Angewandte Mathematik |
Hochschulgrad | Master of Science (M. Sc.) |
Regelstudienzeit | 4 Semester |
Studienbeginn | Winter- und Sommersemester |
Zulassung | Siehe unten: Vorbildung. Was wird vorausgesetzt? |
Sprachen | Die Lehrveranstaltungen werden in deutscher Sprache gehalten. |
Der Masterabschluss eröffnet gute Chancen auf dem Arbeitsmarkt, ein höheres Einstiegsgehalt und den Zugang in Führungspositionen. Er beinhaltet die Zugangsberechtigung zum Höheren Dienst der Beamtenlaufbahn in Bund und Ländern. Wissenschaftlich Interessierten bietet er die Möglichkeit, Studienfelder in einem anschließenden Promotionsverfahren zu vertiefen und damit eine akademische Laufbahn in Forschung und Lehre einzuschlagen. Der Studiengang qualifiziert u. a. für folgende berufliche Positionen bzw. für Tätigkeiten in folgenden Berufsfeldern: Analysten, Systemarchitekten, Controller, Consulting und Management, Softwareentwicklung, Risikomanagement, Fertigungskontrolle, Produktionsinspektion, wissenschaftliche Tätigkeiten im fachlichen Kontext (z.B. in Research-Abteilungen von Banken, Versicherungen und Industrieunternehmen).
Die Regelzulassungsvoraussetzung für den Master Studiengang ist ein guter oder sehr guter qualifizierter Bachelor- oder Diplomabschluss auf dem Gebiet der Mathematik mit einem Umfang von mindestens 180 Leistungspunkten. Bei Studienabschlüssen, welche die vorstehenden Kriterien nicht erfüllen, führt der Prüfungsausschuss individuelle Eignungs- und Feststellungsprüfungen durch. Eine detaillierte Darstellung der Zulassungsvoraussetzungen finden Sie in den Besonderen Bestimmungen der Prüfungsordnung (BBPO).
Interessierte müssen sich unter Einhaltung einer Frist bewerben. Die Zulassung regelt der §6 in Verbindung mit der Anlage 4 der Besonderen Bestimmungen der Prüfungsordnung für den Masterstudiengang. Eine zahlenmäßige Zulassungsbeschränkung existiert nicht.
Die erforderlichen Qualifikationen und Kompetenzen vermitteln die Module des Masterstudiengangs Angewandte Mathematik. Diese Studiumseinheiten können Lehrveranstaltungen, Projektarbeit oder Laborphasen einschließen.
- Modulhandbuch Master Angewandte Mathematik
- Prüfungsordnung Master Angewandte Mathematik
Das Modulhandbuch wurde amtlich im Hochschulanzeiger 2023, die BBPO im Hochschulanzeiger 2024 veröffentlicht.
Erste Anlaufstelle für die meisten Fragen zum Studium ist das Student Service Center, kurz SSC. Neben der allgemeinen Studienberatung und Auskunft zu den Details des Bewerbungsverfahrens gibt es hier auch Beratung zur Organisation oder Finanzierung des Studiums. Student Service Center (SSC)
Bei Fragen zum Studiengang wenden Sie sich an Prof. März.
Sobald man mit dem Studium begonnen hat, sind das die vermutlich wichtigsten Seiten:
Über den Link my.h-da (ist auch unter Quicklinks hinterlegt) kommst Du zum Hochschulinformationssystem für Studierende. Hier kannst Du
- alle benötigten Bescheinigungen (Studienbescheinigungen, Bafög-Bescheinigung und die Quittung über die entrichteten Beiträge) selbst ausdrucken.
- Informationen zu Ihren Prüfungen und Noten einsehen.
- sich für Prüfungen an- oder auch wieder abmelden.
- sich für Veranstaltungen eintragen.
- Ihren Studiengangplan und das Vorlesungsverzeichnis einsehen.
- sich Ihren individuellen Stundenplan zusammenstellen.
Unter www.h-da.de/tutorials findest Du Kurzanleitungen für Prüfungsanmeldungen, Noteneinsichten u.v.m.
Semestertermine: Hier sind zentral für alle Studiengänge die Termine für Klausuren und Veranstaltungen hinterlegt. Auch diese Seite ist über Quicklinks direkt zu erreichen.
Stundenpläne: Auf diese Seite sind für alle Studiengänge die Links zu den PDFs mit den aktuellen Stundenplänen gelistet.
Teilzeitstudium
Der Masterstudiengang kann grundsätzlich auch in individueller Studienausgestaltung als Teilzeitstudium (50%) durchgeführt werden, indem die Lehrveranstaltungen in einer zeitlich modifizierten Form absolviert werden.
Weitere Informationen bekommen Sie im Student Service Center (SSC) oder bei Prof. März.
Master-Abschlussarbeiten Angewandte Mathematik
- Resourceneinsatzplanung zur Erstellung ertragsoptimierter Erntepläne
- Multiagenten Reinforcement Learning zur Steuerung von Portalsystemen
- Kündigungsprognosen mittels Methoden des Data Mining und Machine Learning
- Bayesian Optimization with Comparison Data
- Generierung eines Busliniennetzes basierend auf simulierten Mobilitätsdaten
- Optimierung der Ferntransporte in einem postalischen Distributionsnetzwerk – Implementierung und Auswertung eines gemischt-ganzzahligen Optimierungsmodells
- Erstellung eines Kostenverrechnungsmodells für die Wert- und Brandschutzumlage des Industrieparks Weinheim unter Berücksichtigung risikomathematischer Methoden
- Numerische Studie zu den Möglichkeiten der Steuerung der Zugfestigkeit der Mörtelsysteme für chemische Anker (HY)
- Identifying synthetic lethal partners for topoisomerase genes TOP1 & TOP2A
- Statistische Testverfahren zur Überprüfung der Angemessenheit der Heubeck-Richttafeln 2018 G für Aktiven- und RentnerbeständeKenngrößenbestimmung für geschlossene Mehrprodukt-Warteschlangennetzwerke mit Batch-Processing
- Die Hilpert-Transformation als beschränkter Operator von Lp nach Lp
- Analysis of Adversarial Examples with Layerwise Relevance
- Polygone und die Schwarz-Christoffel-Transformation
- Numerische Simulation der Abkühlung eines C/C-Verbundes
- Analyse von numerischen Verfahren zur Arbitrage Optimierung: Ein Vergleich zwischen Monte Carlo basierten Methoden und quanten-inspirierten Simulated Annealing
- Analyse des IPCW-Ansatzes zur statistischen Auswertung rechtszensierter Daten mit einer Anwendung auf Registerdaten zu Organtransplantationen
- Statistische Prognose von Studienerfolgen aus Zwischenanalysen und externen Studiendaten
- Liquidität in Kryptomärkten
- In silico Identifikation und Evaluierung synthetisch letaler Interaktionen von Nuklearen
- Analyse des IPCW-Ansatzes für Machine Learning Verfahren mit einer Anwendung auf Nierentransplantationsdaten
- Optimierung der Ferntransporte in einem postalischen Distributionsnetzwerk – Implementierung und Auswertung eines gemischt-ganzzahligen Optimierungsmodells
- Algorithmen zur Lösung des 2. Median-Problems auf Graphen großer Dimensionen
- Numerical calculation of the distribution of the false discovery proportion in the two-groups mixture model
- Analyse der Schadeninflation bei Großschäden in der Kraftfahrt-Haftpflichtversicherung
- Nichtlineare restringierte Optimierungsverfahren
- Spezielle Methoden des Operational Risk Management
- Interpolationsmethoden in der Exposure-Simulation bei Zinsderivaten
- Post-Crisis-Modellierung von Volatilitätsoberflächen für Swaptions
- Theorie und Implementierung eines parameterfreien kombinatorischen Hypothesentests auf der Basis von Iterationen
- Bewertung von Unternehmen unter Verwendung stochastischer Ansätze
- Asymptotische Eigenschaften der Operatoren von Kis und Vértesi
- Multivariate Verfahren im Rahmen der Geschäftsplanung
- Receiver Operation Characteristic in der stochastischen Signalerkennung
- Sicherheitsmargen in Unisex-Rechnungsgrundlagen für Rentenversicherungen
- Identifikation, Simulation und optimale Kontrolle eines Lastkran-Labormodell
- Entwicklung eines Prognosemodells für ein Call-Center
- Potenzreihenansatz zur Lösung linearer Differentialgleichungen mit polynomiellen Koeffizienten
- Ein statistisches Verfahren zur Reproduzierbarkeit experimenteller Testergebnisse
- Bestimmung der optimalen Behälteranzahl der Gepäckförderanlage des Flughafens Frankfurt mit Hilfe der Clusteranalyse
- Varianten eines parameterfreien kombinatorischen Testverfahrens
- Predictive Analytics zur Absatzplanung im Schienengüterverkehr
- Analyse eines SHIFTED - SABR - MODELLS
- Entwicklung eines Forecast und eines Alerting Frameworks für die vom Billing-System bepreisten Telefon-Nutzungsdaten zur Sicherstellung der zeitgerechten Fertigstellung des Monatsabschlusses
- Post-Crisis-Risikomanagement von Verbindlichkeiten ohne feste Laufzeiten
- Alternative Einlagenzinsmodelle für Verbindlichkeiten ohne feste Laufzeiten
- Quo Vadis interne Modelle?
- Stochastische Unternehmensbewertung
- An interest rate model for non-maturing deposits based on neutral differential equations
- Das Varianz-Gamma-Modell: Eine theoretische Einführung und Tests an deutschen Aktienindices
- Stochastische Signalerkennung
- An Interest Rate Model for Non Maturing Deposits based on Delayed Differential Equations
- Vergleich von Verfahren zur Spätschadenreservierung
- Adaptives Verfahren zur Messung des Marktpreisrisikos in der DZ BANK AG
- Dynamische Multiprojektplanung im Backoffice
- Implementierung von Unisex-Rechnungsgrundlagen in der betrieblichen Altersversorgung
- Fraktionale partielle Differentialgleichungen mit Anwendung auf das Black-Scholes-Modell
- Verschnittoptimierung in der Papierindustrie: Modellformulierungen realer Problemstellungen und exakte Lösungsverfahren
- Backtesting des Expected Shortfall Risikomaßes
- Statistischer Vergleich von Ratings der drei größten Agenturen
- Vier Szenarien für die Annahmestichprobenprüfung bei attributiven Merkmalen
- Exakte Testverteilungen für zwei nichtparametrische Hypothesentests von Wilcoxon
- Vergleich verschiedener Ansätze zur Entwicklung von Upliftmodellen zur Kundenselektion
- Stilisierte Fakten im Kontext theoretischer Kapitalmarktmodelle
- Risikokapitalberechnung unter Solvency II: Welche Fehler bringt die Verwendung falscher Abhängigkeitsstrukturen mit sich?
- Bewertung von Kapitalmarktfloatern unter dem Baseler Zinsschock
- Run Test: Theoretische Verteilung der Runs up-and-down bei Systemen ohne Gedächtnis
- Statistische Analyseverfahren zur Bewertung von Faktoren der zustandsorientierten Instandhaltung baulicher und technischer Anlagen von Personenbahnhöfen
- Total valuation adjustment including bilateral counterparty credit risk and funding costs
- Simulationstechniken und die Markov Chain Monte Carlo Methode
- Ist-Analyse gängiger Verfahren zur Betrachtung von zukünftigen Liquiditätsrisiken auf Grundlage der Extremwerttheorie
- Modellierung von Sicherheiten in der Exposure-Messung
- Szenariogenerierung zur Bewertung zukünftiger Zins- und Aktien-Cashflows
- Verwendung von Wavelet-Verfahren bei der Parameteridentifikation der Black-Scholes Differentialgleichung
- Indikatorgestützte Ermittlung landesspezifischer Servicekosten
- Verdichtung von Versicherungsbeständen als quadratisches Optimierungsproblem
- Bewertung von Credit Default Swaps unter Berücksichtigung des Credit Valuation Adjustments und Wrong Way Risk
- Analyse des Ansatzes von Hull&White zur Ermittlung des Wrong Way Risks in der Kontrahentenrisikomessung
- Auswertung von Fahrdaten aus der chinesischen Felderprobung mittels multivariater statistischer Methoden
- Funding Value Adjustment (FVA) für Zinsprodukte
- Analytische Approximation des Credit Valuation Adjustments
- Orthogonale Regression und Regression nach Deming
- Sensitivitätsanalysen des Partiellen Internen Modells der Mannheimer Versicherung unter Solvency II
- Anfangsstörungen für Vorhersagen in nichtlinearen dynamischen Systemen
- Schätzung des Value-at-Risk durch Methoden der Extremwerttheorie: Vergleich zwischen der ultimate und der penultimate Approximation
- Empirische Analyse von Anwartschaftsbarwerten in der betrieblichen Altersversorgung bei stochastischer Variation von Bewertungsprämissen
- Strategien zum Hedging des Credit Valuation Adjustments und Anwendung auf ein Musterportfolio
- Receiver Operating Characteristic, Gini-Koeffizient und Payoff-Matrix als Optimierungstools der logistischen Regression und der Diskriminanzanalyse
- Analyse des Berechnungsverfahrens von Planblockzeiten unter Berücksichtigung treibstoffoptimierten Fliegens
- Analyse und Entwicklung eines SPC-Systems in der Herstellung von Labordiagnostika
- Statistische Analysen zur automatischen Fahrgastzählung
- Clusteranalyse von börsennotierten Unternehmen
- Auswirkungen der AIFM-Richtlinie auf das deutsche Investmentrecht und das Risikocontrolling der BNY Mellon Service KAG
- Entwicklung und Bewertung eines Prognosemodells über die erwartete Menge an aufzubauenden Frachteinheiten im Abfertigungsbereich eines Luftfrachtunternehmens
- Statistische Prozesslenkung der automatischen optischen Inspektion in der Elektronikkartenfertigung der SICK AG
- Multivariate statistische Verfahren zur Entwicklung von Adress-Scores
- Zusammenhangsanalysen in der SMD-Prozessfertigung der SICK AG
- Qualitative und quantitative Analysen des Dynamic Risk Managements
- Spatial Data Analysis mit SAS: Analyse von Inzidenzdaten aus dem Gesundheitsbereich
- Mathematische Definition, statistische Beschreibung und Analyse von Kundennutzungsprofilen
- Das Kontrahentenrisiko und die besondere Rolle der Besicherung und des Wrong Way Risks
- Valuation of Counterparty Risk for Commodity Derivatives
- Market Implied Ratings für Corporate Bonds
- A Market Model Approach for Measuring Counterparty Credit Risk of Interest Rate Derivatives
- Identifikation stabiler Knoten in dynamischen Netzen
- Quantitative Analyse von Commodity Futures bei MVV Energie AG
Kontakt
Studienfachberatung
Sekretariat
Öffnungszeiten Sekretariat | |
|---|---|
Mo: | Termin nach Vereinbarung |
Di: | Termin nach Vereinbarung |
Mi: | 09:00 - 14:00 Uhr offene Sprechstunde |
Do: | 09:00 - 14:00 Uhr offene Sprechstunde |
Fr: | Termin nach Vereinbarung |
Infos kompakt
Studiengangsflyer
Stundenpläne
Termine und Fristen
Bekanntmachungen PA
Moodle-Kurse
Prüfungsordnung 2018 (in der 2023 aktualisierten Fassung)
- Prüfungsordnung Master Angewandte Mathematik
- Modulhandbuch Master Angewandte Mathematik
- Allgemeine Bestimmungen für Prüfungsordnungen ABPO