3. Ohmsches Gesetz

In einem elektrischen Widerstand $R$ werden die Elektronen gebremst, ähnlich wie Wasser, das sich durch einen Schwamm quälen soll. Das Bremsvermögen des Widerstands $R$ ist definiert als Verhältnis aus Spannung $U$ und Stromstärke $I$:

$R = \frac {U}{I}; \qquad \text{Einheit: } 1 \Omega = \frac{1 V}{1 A}$

Darstellung eines einfachen Stromkreises, bestehend aus Spannungsquelle und einem Widerstand.

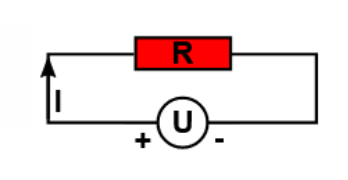
Dieses Ohmsche Gesetz ist die Definition des elektrischen Widerstands. Der anschauliche Gehalt des Ohmschen Gesetzes ist am besten in der Form:

$ I = \frac{U}{R}$

zu erkennen: Die Stromstärke $I$  ist proportional zur Spannung $U$ und umgekehrt proportional zum Widerstand $R$. Noch anders formuliert:

$ U = R \cdot I$

Diese Gleichung besagt: die Spannung, die an den Enden des Widerstands gemessen wird (der 'Spannungsabfall') ist proportional zu Strom und Widerstand. Bei Metallen ist $R$  nur von der Temperatur anhängig, bei Halbleitern gibt es beliebig abenteuerliche Anhängigkeiten.

Wenn zwei Widerstände 'in Reihe' (d. h. hintereinander) geschaltet werden, fließt durch beide Widerstände der selbe Strom. Die Gesamtspannung, mit der diese Reihenschaltung versorgt wird, teilt sich auf die beiden Widerstände auf. Mit einem Voltmeter kann man jeweils zwischen den Enden jedes Widerstands eine Spannung messen, den sog. 'Spannungsabfall' an dem Widerstand.

Wegen der Energieerhaltung muss die Summe der Einzelspannungen gleich der Gesamtspannung sein:

Ausschnitt aus einem Stromkreis mit zwei hinter einander geschalteten Widerständen R1 und R2.

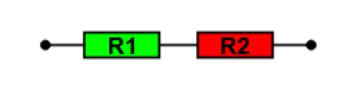
$I_1 = I_2; U_1 + U_2 = U_{gesamt}$

Außerdem gilt für jeden Einzelwiderstand das Ohmsche Gesetz:

$U_1 = R_1 \cdot I; \qquad U_2 = R_2 \cdot I$

Also ist:

$U_{gesamt} = U_1 + U_2 = (R_1 + R_2) \cdot I = R_{gesamt} \cdot I$

Die Reihenschaltung verhält sich so, als sei ein einzelner Widerstand im Stromkreis (der 'Gesamtwiderstand' oder 'Ersatzwiderstand'), dessen Wert gleich der Summe der Einzelwiderstände ist.

Ausschnitt aus einem Stromkreis mit zwei hinter einander geschalteten Widerständen R1 und R2, die zu einem Gesamtwiderstand R addiert werden können.

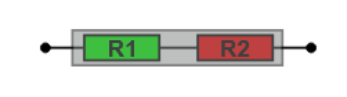
$R_{gesamt} = R_1 + R_2$

Wenn zwei Widerstände parallel geschaltet sind, liegt an ihnen dieselbe Spannung. Der Strom teilt sich jedoch an einer Verzweigungsstelle ('Knoten') auf die beiden Widerstände auf.

Die Skizze zeigt, wie sich in einem Stromkreis mit zwei parallelen Widerständen R1 und R2, die unterschiedlich groß sind, der Strom aufteilt.
Die Ströme teilen sich im Verhältnis der Kehrwerte der Widerstände ('Leitwert') auf. Hier gilt z. B.: R1 > R2

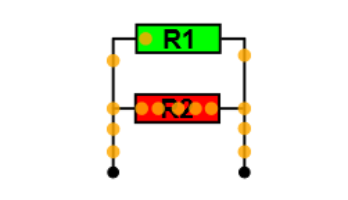
Wieder gilt für jeden Widerstand einzeln das Ohmsche Gesetz. Wegen der Ladungserhaltung ist die Summe der Ströme, die durch die einzelnen Widerstände fließen, gleich dem Gesamtstrom.

$U_1 = R_1 \cdot I_1; U_2 = R_2 \cdot I_2$

$I_1 + I_2 = I_{gesamt}; U_1 = U_2 = U$

Also ist:

$I_{gesamt} = I_1 + I_2 = \frac{U}{R_1} + \frac{U}{R_2} = U \cdot (\frac{1}{R_1} + \frac{1}{R_2}) = U \cdot \frac{1}{R_{gesamt}} = \frac{U}{R_{gesamt}}$

Die Parallelschaltung verhält sich so, als sei ein einzelner Widerstand im Stromkreis (der 'Gesamtwiderstand' oder 'Ersatzwiderstand'). Die Summe der Kehrwerte der Einzelwiderstände ist gleich dem Kehrwert des Gesamtwiderstands. Der Gesamtwiderstand ist kleiner als jeder der beiden Einzelwiderstände.

Die Skizze zeigt symbolisch, wie sich bei der Parallelschaltung von zwei Widerständen R1 und R2 der Gesamtwiderstand R berechnet.

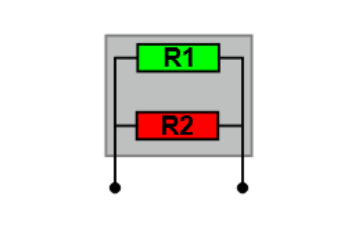
$\frac{1}{R_1} + \frac{1}{R_2} = \frac{1}{R_{gesamt}}$