5. Kinematik
Technische und natürliche Vorgänge laufen im Raum und in der Zeit ab. 'Kinematik' ist die systematische Beschreibung solcher Vorgänge mit Begriffen wie Ort, Zeit, Geschwindigkeit, Beschleunigung. Die Ursachen dieser Vorgänge werden dabei nicht behandelt, ähnlich wie ein Fahrplan den Ort eines Zuges zu jedem Zeitpunkt seiner Fahrt beschreibt, aber keine Auskunft über das Antriebsaggregat der Lokomotive gibt.
Bei vielen Größen in der Kinematik spielt die Richtung eine Rolle. Eine gerade Wegstrecke kann in zwei Richtungen durchlaufen werden. Die zugehörige Verschiebung im Raum ist eine gerichtete Größe. Bei einer Bewegung mit konstanter Geschwindigkeit auf einer Geraden müssen Sie nicht nur den Betrag, sondern auch die Richtung der Geschwindigkeit angeben. Gerichtete Größen werden als Vektoren bezeichnet, im Unterschied zu Skalaren wie z. B. der Druck, die vollständig durch ihren Betrag beschreiben werden.
In diesem Vorkurs werden einige Beispiele aus der Kinematik behandelt, so dass Sie von Beginn an in der Physikvorlesung verstehen können, wie Koordinatensysteme, Vektoren und der Parameter Zeit verwendet werden. Das Gesamtgebiet der Kinematik ist wesentlich umfangreicher als das, was wir Ihnen in diesem Vorkurs zeigen wollen.
Entsprechend werden Sie in der Mathematikvorlesung einen systematischen Zugang zu einem Vektorbegriff kennenlernen, der weit über das hinausgeht, was Sie im Kapitel Vektoren lesen können.
5.1 Ortsvektoren
Die Bewegung eines Körpers im Raum können Sie beschreiben, indem Sie auflisten, an welchen Punkten sich der Körper zu welchen Zeiten befindet.
Mit der Zeitangabe gibt es selten Probleme: die Zeit 'fließt' in einer Richtung (in die Zukunft), und praktisch jeder hat eine Armbanduhr. Als 'Zeitnullpunkt' wird in den meisten Kulturen Christi Geburt benutzt, alles andere regelt der Gregorianische Kalender. Im Jet-Zeitalter muß man allerdings auf die Zeitzonen achten: Jede Zeitzone hat für den aktuellen Tag ihren eigenen Zeitnullpunkt.
Wenn Sie zur Zeitmessung bei einem Vorgang eine Stoppuhr verwenden, z. B. bei einem 100m-Lauf, dann müssen Sie ebenfalls den Nullpunkt Ihrer Zeitmessung eindeutig definieren, um Mißverständnisse zu vermeiden. Für die eindeutige Zeitangabe benötigen Sie also zwei Informationen: einen Zeitnullpunkt und eine Zeitspanne, die den Abstand des Ereignisses vom Zeitnullpunkt angibt.
Heute tragen schon viele Menschen eine Armbanduhr, die nicht nur die Zeit, sondern über ein Satellitenmessnetz wie das GPS (Global Positioning System) auch den Ort in der Nähe der Erdoberfläche anzeigt. Damit kann man nicht nur in der Zeit, sondern auch im Ort 'pünktlich' sein!
Für die Ortsangaben benötigen Sie mehrere Informationen. Zunächst müssen Sie einen Bezugspunkt im Raum angeben, den 'Nullpunkt' oder 'Ursprungspunkt'. Dann müssen Sie drei Richtungen im Raum festlegen, die 'Koordinatenachsen'. Beliebt ist ein System aus drei Richtungen, die jeweils aufeinander senkrecht stehen und durch Geraden charakterisiert werden, die durch den Ursprungspunkt verlaufen. Diese drei Achsen werden meist mit x, y, z bezeichnet.
Die Wegbeschreibung zu einem bestimmten Punkt im Raum lautet dann z. B. 'Gehen Sie vom Ursprungspunkt aus 10m in Richtung der x-Achse, von dort aus 20m entgegengesetzt zur Richtung der y-Achse und dann noch 15m in Richtung der z-Achse.' Das ist so ähnlich wie eine Anweisung zur Schatzsuche: 'Gehen Sie von der Eiche aus 10m nach Süden, dann 20m nach Westen, und schauen Sie im hohlen Stamm des Baums in 15m Höhe nach.'
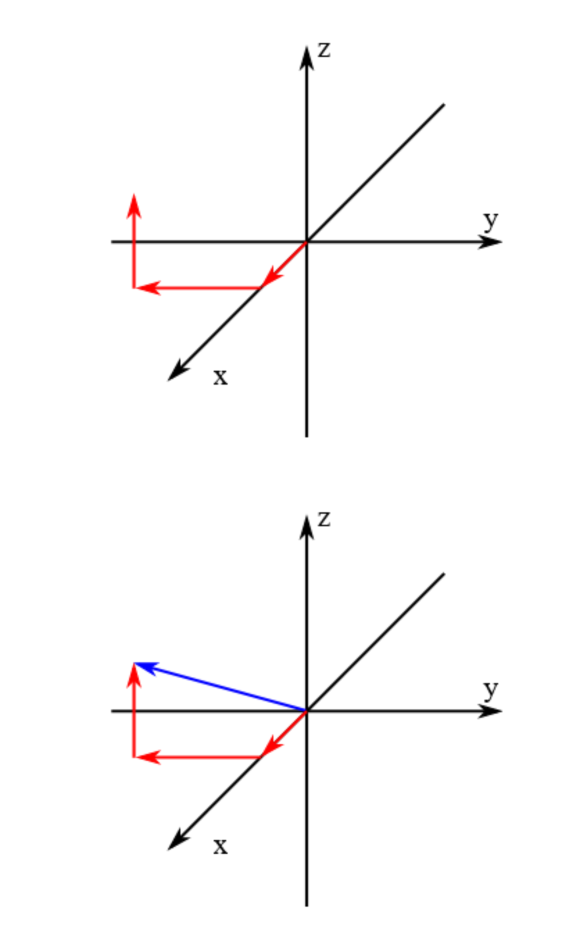
Beachten Sie bitte, dass Sie nicht nur den Nullpunkt und die Abstände, sondern auch die Richtungen benötigen, in die Sie gehen müssen, also die Orientierung der x, y und z-Achse.
Statt längs der drei Achsenrichtungen zu gehen, hätten Sie auch direkt auf einer geraden Linie vom Ursprungspunkt zum Zielpunkt gehen können. Einen Punkt im Raum können Sie also durch eine Verschiebung vom Nullpunkt zu diesem Punkt charakterisieren.
Diese Verschiebung zeichnet man als Pfeil, der im Ursprungspunkt beginnt und dessen Spitze im Zielpunkt liegt. Die Länge des Pfeils ist der Abstand zwischen Ursprungspunkt und Zielpunkt. Die Richtung des Pfeils kennzeichnet die Richtung, in der Sie den Ursprungspunkt bewegen müssen, um zum Zielpunkt zu kommen. Dieser Pfeil, der im Ursprungspunkt beginnt, ist der Ortsvektor des Punkts.
Machen Sie sich klar, dass der Ortsvektor derselbe bleibt, wenn Sie sich auf andere Richtungen für die Koordinatenachsen einigen. Solange Sie den Nullpunkt des Systems feshalten, bleibt der Pfeil im Raum liegen. In vielen Fällen können Sie eine Situation bereits analysieren, wenn Sie lediglich diese geometrische Vorstellung eines Vektors benutzen und Vektoren 'hinzeichnen'.
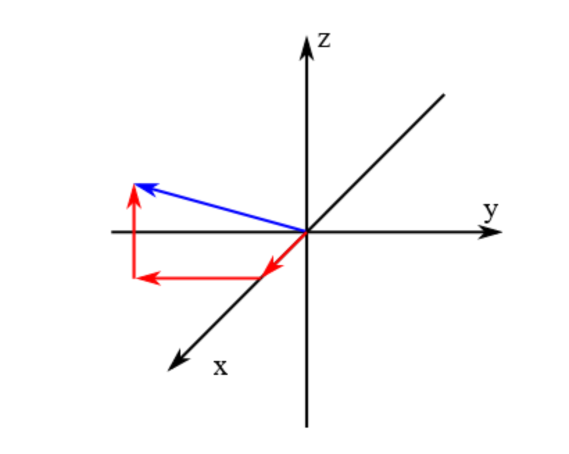
Der Ortsvektor eines Punktes wird mit $\textbf{r}$ bezeichnet. Die Länge eines Vektors (ohne Vorzeichen!) ist sein Betrag, bezeichnet mit $| \textbf{r} |$ oder einfach mit r. Der Betrag des Ortsvektors ist sein Abstand vom Nullpunkt.
In früheren Texten finden Sie manchmal noch einen Buchstaben mit einem kleinen Pfeil darüber als Kennzeichnung eines Vektors $\vec{r}$. Diese Notation wird heute nur noch handschriftlich verwendet, z. B. in der Vorlesung an der Tafel. In Texten und Formeln sind Vektoren entsprechend den Empfehlungen der Physikalisch-Technischen Bundesanstalt generel fett (und meist auch kursiv) gesetzt.
Achten Sie deshalb in Lehrbüchern und in Textdokumenten auf kursiv fett gesetzte Buchstaben, die Vektoren symbolisieren, und verwechsln Sie sie nicht mit den lediglich kursiv gesetzten Beträgen.
Wenn Sie mit Vektoren rechnen wollen, müssen Sie irgendwann auf ihre 'Koordinatendarstellung' zurückgreifen. Unter Bezug auf das vorher festgelegte Koordinatensystem geben sie dann einfach die drei Werte an, die die nacheinander auszuführenden Verschiebungen längs der Koordinatenachsen bis zum Zielpunkt beschreiben ('10 m in Richtung der x-Achse...'). Ein Wert mit negativem Vorzeichen bedeutet, dass Sie entgegengesetzt zur festgelegten Richtung der Koordinatenachse gehen müssen. Meistens ordnet man die 'Koordinaten' in einer Spalte an und setzt eine Klammer herum:
$$\textbf{r} = \left( \begin{array}{c} x \\\ y \\\ z \end{array}\right) = \left( \begin{array}{c} 10m \\\ -20m \\\ 15m \end{array}\right) $$
Gebräuchlich, weil einfacher zu schreiben ist aber auch:
$$\textbf{r} = \left(x,y,z\right) =\left(10m, -20m,15m\right)$$
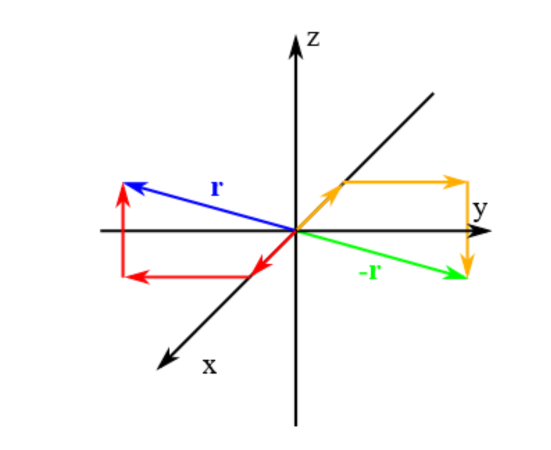
Der Vektor $-\textbf{r} =\left(-10m, 20m,-15m\right)$ zeigt im Raum in die Gegenrichtung von $\textbf{r}$. Die Vektoren sind gleich lang, aber entgegengesetzt gerichtet.
Wenn Sie auflisten wollen, an welchen Punkten sich ein Körper im Raum zu welchen Zeitpunkten befindet, dann können Sie diese Liste in Form der Funktion $\textbf{r}\left(t\right)$ hinschreiben. diese Funktion beschreibt die Bahn des Objekts mit der Zeit als Parameter.
Aus der Diskussion über den Ortsvektor konnten Sie entnehmen, dass der Vektor selbst unabhängig vom Koordinatensystem ist. Lediglich seine Darstellung in Koordinaten ändert sich, wenn Sie das System ändern. Sie sollten immer die Darstellung so einfach wie möglich wählen.
Wenn sich ein Objekt auf einer Geraden bewegt, dann legen Sie die x-Achse Ihres Koordinatensystems direkt in die Bahn des Objekts. Wählen Sie als Richtung der Achse die Richtung, in der sich das Objekt bewegt. Die Koordinaten y und z benötigen Sie jetzt zur Beschreibung gar nicht mehr, sie sind während der ganzen Bewegung null. Es genügt, die Funktion $\textbf{x}\left(t\right)$ anzugeben, zusammen mit den Nullpunkten für die Zeitmessung und für die x-Achse. Da es auf einer Geraden nur zwei mögliche Richtungen gibt, kann der Vektorcharakter des Ortsvektors für einen Punkt auf der x-Achse jetzt durch das Vorzeichen der x-Koordinate ausgedrückt werden.
Analog benötigen Sie zur Beschreibung von Vorgängen, die in einer Fläche ablaufen, nur zwei Koordinaten. Stellen Sie sich z. B. ein Schiff vor, das den Ärmelkanal überquert. Zur Navigation genügt ein Kompass, das Koordinatensystem besteht aus einer x-Achse (der Richtung von Westen nach Osten) und einer y-Achse (der Richtung von Süden nach Norden). Natürlich müssen Sie einen Ursprungspunkt vorgeben, z.B. Dover. Wo Calais liegt, können Sie dann in Bezug auf Dover und die beiden vereinbarten Achsen durch zwei Koordinaten eindeutig angeben. Die dritte Koordinate, die Höhe über der Erdoberfläche, hat auf dem Kanal den Wert Null und ist für die Navigation unbedeutend. Es genügt also, Ortsvektoren in diesem Bezugssystem als $\textbf{r}=\left(x,y\right)$ anzugeben. Nur bei einem 'echten' dreidimensionalen Problem sollten Sie alle drei Ortskoordinaten verwenden und $\textbf{r}$ als $\textbf{r}=\left(x,y,z\right)$ schreiben.
5.2 Vektoraddition
Die Addition zweier Vektoren $\textbf{a}$ und $\textbf{b}$ ist die Anweisung, zunächst mit der für $\textbf{a}$ vorgegebenen Richtung die Länge von $\textbf{a}$ abzuschreiten und anschließend, von der Spitze von $\textbf{a}$ aus, mit der für $\textbf{b}$ vorgegebenen Richtung die Länge von $\textbf{b}$ abzugehen. Die beiden Vektoren werden also aneinandergesetzt. Der Summenvektor zeigt dann vom Anfangspunkt des einen Summandenvektors zum Endpunkt des zweiten Summandenvektors.
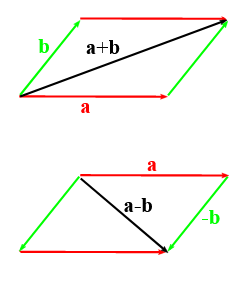
Sie können sofort erkennen, dass $\textbf{a}+\textbf{b}=\textbf{b}+\textbf{a}$ ist. Außerdem sehen Sie, dass der Summenvektor die Diagonale in einem Parallelogramm ist, das durch $\textbf{a}$ und $\textbf{b}$ aufgespannt wird ('Parallelogrammregel der Vektoraddition').
Die Differenz $\textbf{b}-\textbf{a}$ zweier Vektoren $\textbf{a}$ und $\textbf{b}$ ist die Anweisung, den Vektor $-\textbf{a}$ zum Vektor $\textbf{b}$ hinzuzuaddieren. Der Differenzvektor ist die andere Diagonale in einem Parallelogramm, das durch $\textbf{a}$ und $\textbf{b}$ aufgespannt wird.
Einleuchtende Beispiele zur Vektoraddition und -subtraktion finde Sie bei Vorgängen, bei denen Geschwindigkeiten addiert oder subtrahiert werden, z. B. bei einem Flug mit Gegenwind oder Rückenwind oder bei der Überquerung eines Flusses (s. Aufgaben).
Wenn Sie Vektoren in Koordinatenschreibweise darstellen, ist es nicht schwierig, die Vektorsumme in Koordinatenschreibweise auszurechnen ( Tabellen und Formeln - Vektoren).
5.3 Verschiebungsvektoren
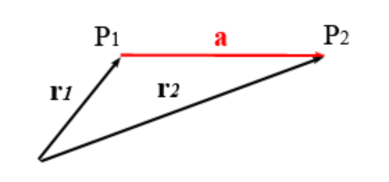
Bei der Bewegung eines Punkts von P1 nach P2 wird der Punkt längs der Verbindungslinie von P1 und P2 verschoben. Diese Verschiebung können Sie durch einen Vektor $\textbf{a}$ beschreiben. Der Verschiebungsvektor $\textbf{a}$ beginnt im Punkt P1, seine Spitze endet im Punkt P2.
Sie können $\textbf{a}$ als die Differenz von $\textbf{r}_1$ und $\textbf{r}_2$ interpretieren:
$\textbf{a} = \textbf{r}_2-\textbf{r}_1$
Entsprechend ist $-\textbf{a} = \textbf{r}_1-\textbf{r}_2$ die Verschiebung für einen Punkt, der sich in Gegenrichtung, also von P2 nach P1 bewegt.
Es gibt verschiedene Möglichkeiten, sich das klarzumachen. Wenn Sie z. B. $\textbf{a}$ parallel zu sich selbst an $\textbf{r}_1$ entlang nach unten ziehen, bis $\textbf{a}$ im Nullpunkt des Koordinatensystems beginnt, dann zeigt die Spitze von $\textbf{a}$ auf einen neuen Punkt im Raum. Diesen Punkt erreichen Sie, indem Sie vom Ursprung aus zum Punkt P2 gehen und von dort aus den Vektor $\textbf{r}_1$ in umgekehrter Richtung durchlaufen, also von der Spitze bis zum Anfang. Sie addieren also den Vektor $-\textbf{r}_1$ zum Vektor $\textbf{r}_2$.
Offenbar dürfen Sie den Vektor $\textbf{a}$ jetzt parallel zu sich selbst frei im Raum verschieben.
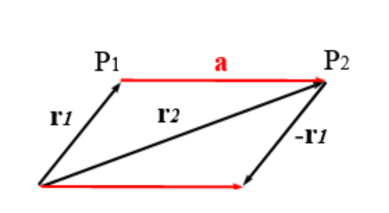
Interpretieren Sie den Vektor $\textbf{a}$ jetzt nicht mehr als Ortsvektor, sondern als Richtungs- und Entfernungsangabe von einem beliebigen Startpunkt aus, also als Vorschrift für eine Verschiebung eines Punktes zu einem anderen Punkt.
Sie können dann sehen, dass die Summe aus $\textbf{r}_1$ und $\textbf{a}$ den Ortsvektor $\textbf{r}_2$ ergibt:
$\textbf{r}_2=\textbf{r}_1 + \textbf{a}$
Das bedeutet: Gehen Sie vom Ursprung aus zur Spitze von $\textbf{r}_1$ und von dort aus in die von $\textbf{a}$ vorgegebene Richtung so weit, wie durch die Länge von $\textbf{a}$ angegeben. Dann kommen Sie zur Spitze von $\textbf{r}_2$.
Ein irgendwo hingezeichneter Pfeil, dessen Länge und Richtung die Verschiebung $\textbf{a}$ beschreibt, repräsentiert graphisch die gesamte Klasse aller Verschiebungen gleicher Länge und Richtung wie $\textbf{a}$, die Sie mit den Punkten des Raumes durchführen können. Der Vektor $\textbf{a}$ 'ist' diese ganze Klasse von gleichartigen Verschiebungen.
Der Vektor $\textbf{a}$ ist in diesem Sinne völlig unabhängig vom gewählen Koordinatensystem, auch von dessen Ursprungspunkt. Er repräsentiert eine Verschiebung mit willkürlichem Anfangspunkt. Viele physikalische Größen haben diese Eigenschaft, z. B. die Geschwindigkeit. Wenn Sie mit Ihrem Auto über die Autobahn fahren, dann bleiben Betrag und Richtung der Geschwindigkeit dieselbe, unabhängig davon, in welchem Koordinatensystem Sie den Vorgang beschreiben.
Ein Repräsentant von $\textbf{a}$ ist der Ortsvektor, der dieselbe Richtung und dieselbe Länge wie $\textbf{a}$ hat, aber im Ursprung des Koordinatensystems beginnt. In diesem Koordinatensystem können Sie $\textbf{a}$ durch die Koordinatenangabe (x,y,z) des zugehörigen Ortsvektors quantitativ beschreiben. Der Verschiebungsvektor $\textbf{a}$ und der Ortsvektor $\textbf{a}$ sind sich sehr ähnlich, aber begrifflich verschieden.
Ortsvektoren dürfen Sie nicht verschieben, sie beginnen immer im Koordinaten- Ursprung. Kräfte dürfen Sie in bestimmten Situationen verschieben, aber u. U. nur 'längs ihrer Wirkungslinie', d.h. auf der Geraden, längs derer der Vektorpfeil zeigt. Sie müssen also jeweils wissen, ob Sie eine vektorielle Größe frei verschieben dürfen oder ob sie irgendwo 'angebunden' bleiben muss. Was Sie mit welcher vektoriellen Größe machen dürfen und was nicht, werden Sie an der entsprechenden Stelle in der Physikvorlesung hören.
5.4 Das Überlagerunsprinzip
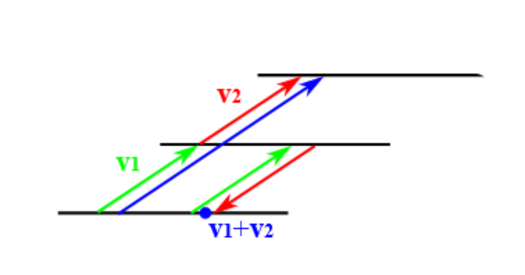
Wenn Sie z. B. auf einer Rolltreppe nicht nur stehen, sondern zusätzlich aufwärts laufen, dann bewegen Sie sich gegenüber dem Gebäude mit der Summe der Geschwindigkeiten der Einzelbewegungen - inklusive Vorzeichen. Wenn Sie z. B. abwärts mit derselben Geschwindigkeit laufen, mit der sich die Rolltreppe aufwärts bewegt, dann bleiben Sie in Bezug auf das Gebäude am selben Punkt im Raum stehen, Ihre Geschwindigkeit ist null.
Der Geschwindigkeitsvektor Ihrer Gesamtbewegung ist die Vektorsumme der Geschwindigkeitsvektoren der Einzelbewegungen.
Umgekehrt können Sie eine beliebige Bewegung in Teilbewegungen aufspalten. Wenn Sie z.B. unter einem Winkel von 30° zum Ufer durch einen Kanal schwimmen, können Sie die Bewegung in Teilbewegungen parallel und senkrecht zum Ufer zerlegen.
Die Bewegung parallel zur Uferlinie entspricht der Bewegung, die ein Beobachter ausführt, der am Ufer entlanggeht und immer auf Ihrer Höhe bleibt.
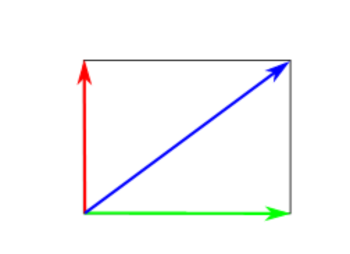
Die Bewegung senkrecht zur Uferlinie entspricht der Bewegung, die ein Beobachter ausführt, der den Kanal gleichzeitig mit Ihnen auf dem kürzesten Weg durchschwimmt und dabei immer auf Ihrer Höhe bleibt.
Die Aufspaltung der Bewegung entspricht also der Projektion Ihrer Bewegung auf die beiden Achsen parallel und senkrecht zum Ufer. Die Teilbewegungen können Sie duch Geschwindigkeitsvektoren charakterisieren, deren Vektorsumme zu jedem Zeitpunkt Ihre Gesamtgeschwindigkeit ergibt.
Wenn ein Körper gleichzeitig mehrere Bewegungen ausführt, dann überlagern sich diese Bewegungen zu einer Gesamtbewegung, ohne sich gegeneitig zu stören. Dieses Überlagerungsprinzip oder Superpositionsprinzip ist der Grund dafür, dass Bewegungen in der Kinematik sehr elegant durch Vektoren beschrieben werden können.
In der Kinematik wird dieses Prinzip an vielen Stellen verwendet. In den Aufgaben finden Sie mehrere Beispiele dafür.
5.5 Koordinatensysteme
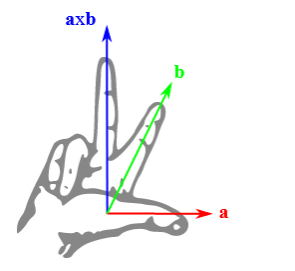
Das kartesische Koordinatensystem besteht aus drei zueinander senkrecht stehenden Koordinatenachsen, die üblicherweise mit x, y und z bezeichnet werden.
Im rechtshändigen Koordinatensystem, das gewöhnlich verwendet wird, sind die Achsen so angeordnet, dass die x-Achse der Richtung des Daumens, die y-Achse der Richtung des Zeigefingers und die z-Achse der Richtung des Mittelfingers der rechten Hand entsprechen, wenn Sie die Finger so ausstrecken, dass Sie senkrecht aufeinander stehen (Drei-Finger-Regel, Schaubild von Qniemiec - LRHREGEL de.png, CC0, Link).
Häufig kommen auch Polarkoordinaten vor, insbesondere bei der Beschreibung von Kreisbewegungen in der Ebene. Anstelle der rechtwinkligen Koordinaten x und y werden der Abstand r vom Ursprungspunkt und der Winkel $\Phi$ in Bezug auf eine festgelegte Achse zur Beschreibung eines Punktes in der Ebene benutzt. Dazu muss der Orientierungssinn der Winkelmessung festgelegt werden. Üblicherweise ist ein Winkel für einen Durchlaufsinn entgegen dem Uhrzeigersinn positiv.
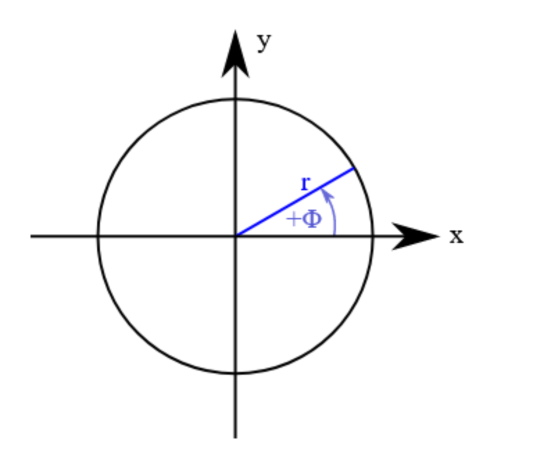
In der Vorlesung werden Sie in der Kinematik bei der Behandlung der Kreisbewegung Polarkoordinaten benutzen.
Polarkoordinaten (Kugelkoordinaten) werden auch für dreidimensionale Probleme benutzt. Ein vermutlich jedem bekanntes Beispiel dafür ist die Ortsbestimmung auf der Erde in Form des Längen- und Breitengrades, gemessen in Bezug auf einen festgelegten Meridian (auf der Erde der Meridian von Greenwich) und in Bezug auf eine Achse durch den Erdmittelpunkt (auf der Erde die Achse durch die Erdpole).
Im allgemeinen Polarkoordinatensystem werden der Längen- und Breitengrad als Azimuthwinkel und Polarwinkel bezeichnet. Die dritte Koordinate ist der Abstand r vom Ursprungspunkt (auf der Erde der Erdmittelpunkt). Auf der Erde hat r an allen normalerweise zugänglichen Orten annähernd denselben Wert. Obwohl die Erde ein dreidimensionales Objekt ist, genügt deshalb für die Ortsangabe in den meisten Fällen der Längen- und der Breitengrad.
Es gibt weitere, speziellen Problemen angepasste Koordinatensysteme, z.B. Zylinderkoordinaten. Schon die Kugelkoordinaten werden Sie als Studierende, die Physik als Nebenfach hören, vielleicht niemals explizit in der Vorlesung zu sehen bekommen. Angewendet werden sie z.B. in der Elektrodynamik bei der Beschreibung von Abstrahlvorgängen oder in der Quantenmechanik bei der Beschreibung der Zustände der Atomhülle.
Die verschiedenen Koordinatensysteme repräsentieren selbstverständlich dieselben Punkte im Raum bzw. dieselben Vektoren. Lediglich die Zahlenwerte, die die Komponenten numerisch beschreiben, ändern sich beim Wechsel des Systems. Die Angaben für die Koordinaten eines Punktes in verschiedenen Systemen kann mann ineinander mit Hilfe von Koordinatentransformationen umrechnen. Dieses Thema wird in der Mathematikvorlesung behandelt.
5.6 Geschwindigkeitsvektor
Die mittlere Geschwindigkeit ist die innerhalb eines Zeitraums $\Delta t$ zurückgelegte Strecke $\Delta s$ dividiert durch diese Zeitintervall. Wenn Sie ein immer kleineres Zeitintervall um einen bestimmten Zeitpunkt t herum betrachten, ändert sich die mittlere Geschwindigkeit immer weniger, sie nähert sich einem Grenzwert. Diesen Grenzwert können Sie schließlich dem Zeitpunkt t selbst zuordnen.
Dieser Grenzwert wird Momentangeschwindigkeit oder Geschwindigkeit zum Zeitpunkt t bezeichnet. Er wird mit $\frac{ds}{dt}$ oder mit einem Punkt über der Funktion $s(t)$ abgekürzt und dann Ableitung nach der Zeit genannt:
$$v(t) = \lim \limits_{\Delta t \to 0} \frac{\Delta s}{\Delta t} = \frac{ds}{dt} =\dot{s}(t) $$
Auch vektoriell ist eine solche Definition sinnvoll: Der Geschwindigkeitsvektor ist der innerhalb eines Zeitraums durchlaufene Verschiebungsvektor vom Punkt P zum Punkt P2 dividiert durch dieses Zeitintervall. Er hat also dieselbe Richtung wie der Verschiebungsvektor.
Der Vektor der Momentangeschwindigkeit ist der Grenzwert, der sich ergibt, wenn Sie für die Berechnung des Geschwindigkeitsvektors das Zeitintervall um einen Zeitpunkt $t$herum immer kleiner werden lassen.
Die Bedeutung dieser Definition können Sie sich jetzt der Reihe nach für die Bewegung auf einer Geraden, für die Bewegung in einer Ebene und dann für den allgemeinen Fall der Bewegung im Raum anschauen.
Bei einer Bewegung längs einer Geraden, z. B. längs der x-Achse, ist die Geschwindigkeit einfach eine Größe mit Vorzeichen. Der Verschiebungsvektor ist $x(t_2) - x(t)$, das Zeitintervall ist $t_2 - t$. Je nach Richtung der Bewegung in Bezug auf die Orientierung der x-Achse kann $x(t_2) - x(t)$ positiv oder negativ sein, entsprechend wird der Geschwindigkeitsvektor parallel oder antiparallel zur Richtung der x-Achse gerichtet sein:
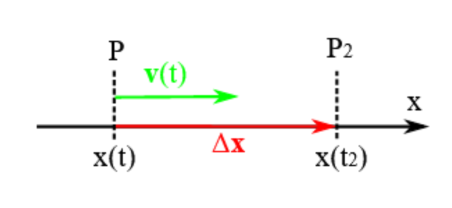
$v(t) = \lim \limits_{\Delta t \to 0} \frac{x(t_2) - x(t)}{t_2 - t} $
Bei einer Bewegung in einer Ebene, die durch ein x-y-Koordinatensystem beschrieben wird, können Sie die Bewegung in eine Teilbewegung längs der x-Achse und in eine Teilbewegung längs der y-Achse aufspalten. Für jede der beiden Teilbewegungen können Sie einen Geschwindigkeitsvektor berechnen. Er ist jeweils entweder parallel oder antiparallel zur entsprechenden Achse gerichtet:
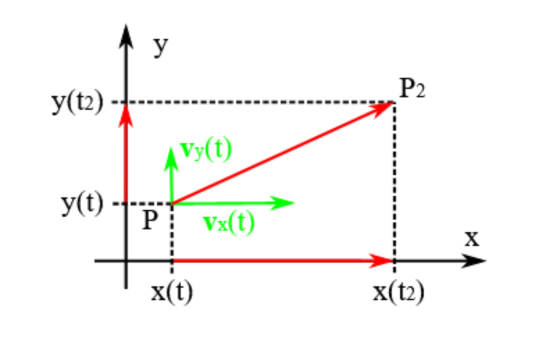
$v_x(t) = \lim \limits_{\Delta t \to 0} \frac{x(t_2) - x(t)}{t_2 - t} $
$v_y(t) = \lim \limits_{\Delta t \to 0} \frac{y(t_2) - y(t)}{t_2 - t} $
Die beiden Geschwindigkeitsvektoren können Sie jetzt vektoriell zum Vektor der Gesamtgeschwindigkeit addieren. In Koordinatenschreibweise schreiben Sie einfach die beiden Geschwindigkeiten längs der x- und der y-Achse untereinander.
Graphisch addieren Sie nach der "Parallelogrammregel".
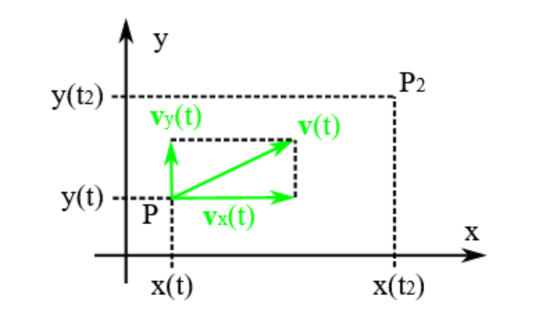
$\textbf{v}(t) = \left( \begin{array}{c} v_x(t) \\\ v_y(t) \end{array} \right)$
Bei der Berechnung des Betrags der Gesamtgeschwindigkeit, also der 'Länge' des Geschwindigkeitsvektors, müssen Sie allerdings die Regeln der Trigonometrie beachten. Bei rechtwinkligen Koordinatensystemen ist es nicht schwierig, den Betrag des Summenvektors aus den Beträgen der Komponentenvektoren zu berechnen (s.Tabellen). Dazu benötigen Sie lediglich den Satz des Pythagoras. Wenn Sie schiefwinklige Koordinaten benutzen, benötigen Sie vielleicht etwas aufwendigere Trigonometrie.
Im dreidimensionalen Raum berechnen Sie den Geschwindigkeitsvektor ähnlich wie bei der Bewegung in der Ebene, es kommt lediglich ein weiterer Summand für die Bewegung längs der z-Achse hinzu:
$$\textbf{v}(t) = \left( \begin{array}{c} v_x(t) \\\ v_y(t) \\\ v_z(t) \end{array} \right)$$
Ausgeschrieben bekommen Sie einen Ausdruck, in dem rechts in der Klammer die Koordinatenschreibweise für die Differenz der Ortrsvektoren der Punkte P2 und P steht:
$$\textbf{v}(t) = \left( \begin{array}{c} v_x(t) \\\ v_y(t) \\\ v_z(t) \end{array} \right) = \left( \begin{array}{c} \lim \limits_{\Delta t \to 0} \frac{x(t_2) - x(t)}{t_2 - t} \\\ \lim \limits_{\Delta t \to 0} \frac{y(t_2) - y(t)}{t_2 - t} \\\ \lim \limits_{\Delta t \to 0} \frac{z(t_2) - z(t)}{t_2 - t} \end{array} \right) = \lim \limits_{\Delta t \to 0} \frac{1}{t_2 - t} \left( \begin{array}{c} x(t_2) - x(t) \\\ y(t_2) - y(t) \\\ z(t_2) - z(t) \end{array} \right)$$
Das entspricht der Definition, die Sie zu Anfang schon gesehen haben: Der Geschwindigkeitsvektor ist der innerhalb eines Zeitraums durchlaufene Verschiebungsvektor von P nach P2 dividiert durch dieses Zeitintervall.
Der Vektor der Momentangeschwindigkeit ist der Grenzwert, der sich ergibt, wenn Sie für die Berechnung des Geschwindigkeitsvektors das Zeitintervall um einen Zeitpunkt $t$ herum immer kleiner werden lassen. Dann wird zwar $\Delta \textbf{r}$ immer kleiner, aber das Verhältnis zu $\Delta t$ wird konstant:
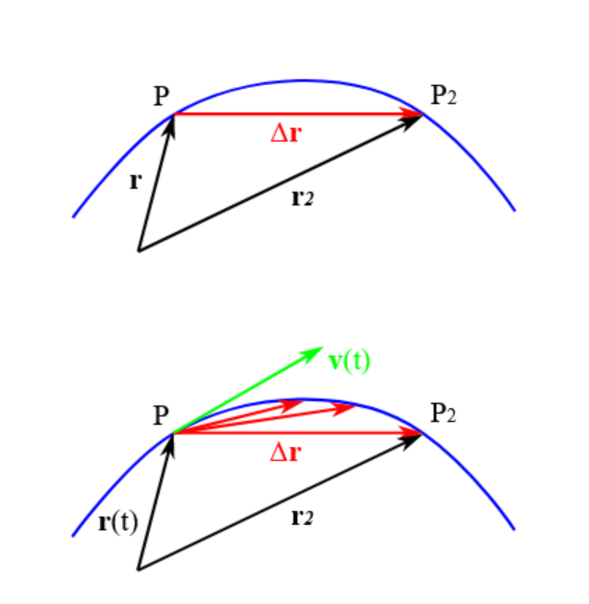
$$\textbf{v}(t) = \lim \limits_{\Delta t \to 0} \frac{\Delta r}{\Delta t} = \frac{dr}{dt} =\dot{r}(t) $$
Der Geschwindigkeitsvektor hat jeweils die Richtung des Verschiebungsvektors. Wenn das Zeitintervall $\Delta t$ immer kleiner wird, wandert der Punkt P2, für den Sie den Verschiebungsvektor von P nach P2 berechnen, immer näher an P heran, und der Geschwindigkeitsvektor hat schließlich die Richtung der Tangente an die Bahnkurve im Punkt P.
Dies ist eine sehr kompakte Schreibweise, die außerdem völlig unabhängig vom gewählten Koordinatensystem ist. Erst wenn Sie mit einer konkreten Darstellung des Vektors rechnen wollen, müssen Sie einen Nullpunkt und Achsenrichtung eines Koordinatensystems festlegen. Alle davorliegenden Rechenschritte können Sie 'abstrakt' mit der Vektornotation hinschreiben.
Wenn Sie dann numerisch rechnen wollen, können Sie sich das dann geeignete Koordinatensystem aussuchen oder evtl. sogar alleine mit geometrischen Überlegungen auskommen, z. B. bei der Addition im Vektorparallelogramm.
Häufig sehen Sie Geschwindigkeitsvektoren in Zeichnungen eingetragen, in denen auch Bahnen in der Ebene oder im Raum vorkommen. Dabei müssen Sie sich darüber klar sein, dass lediglich die Richtung eines Geschwindigkeitsvektors im Raum eine reale Bedeutung hat.
Die Länge des eingezeichneten Vektors symbolisiert seinen Betrag, und Sie müssen vorher vereinbart haben, 'wie viele cm wie viele m/s bedeuten sollen'. Wenn Sie in derselben Zeichnung zwei Geschwindigkeitsvektoren eintragen, dann müssen ihre Längen zueinander im Verhältnis ihrer Beträge stehen. Die Absolutlänge können Sie vollkommen frei wählen, gerade so, wie es zeichentechnisch günstig ist, solange ein Geschwindigkeitsvektor mit dem Betrag 4 m/s doppelt so lang ist wie ein anderer mit dem Betrag 2 m/s.
Mit einigem Aufwand kann man zeigen, dass der Geschwindigkeitsvektor immer tangential zur Bahn eines Körpers gerichtet ist. In der Mathematikvorlesung werden Sie möglicherweise mehr darüber hören.
Für den Start in die Physikvorlesung genügt es, wenn Sie wissen, dass der Geschwindigkeitsvektor sich aus den Teil-Geschwindigkeitsvektoren der Teilbewegungen, aus denen die Gesamtbewegung besteht, durch Vektoraddition ergibt. Längs jeder Achse müssen Sie dann nur noch das Vorzeichen der Teil-Geschwindigkeit als Information über die Richtung der Geschwindigkeit in Bezug auf die verabredete Richtung der Achse interpretieren. Die meisten kinematischen Probleme, z. B. die verschiedenen Varianten des freien Falls wie horizontaler Wurf, schiefer Wurf, senkrechter Wurf können Sie auf diese Weise verstehen und quantitativ behandeln.
Wenn Sie den Begriff der Ableitung einer Funktion kennen, dann haben Sie bestimmt schon gemerkt, dass die Geschwindigkeit für eine Bewegung längs einer x-Achse nichts anderes ist, als die Ableitung der Funktion $x(t)$ nach der Zeit, also die Tangentensteigung im $x(t)$-Diagramm für einen bestimmten Zeitpunkt $t$.
Der Geschwindigkeitsvektor in drei Dimensionen, dargestellt in einem kartesischen Koordinatensystem, enthält als Komponenten nichts anderes als die Ableitungen der Funktionen $x(t)$, $y(t)$ und $z(t)$ nach der Zeit. In diesem Vorkurs setzen wir jedoch keine Differentialrechnung ein. Wenn Ihr Professor im Physikkurs den Zugang zur Kinematik über die Differential- und Integralrechnung wählt, dann sollten Sie sich an Ihre Schulmathematik zu diesem Thema erinnern.
Bei einer Bewegung mit konstanter Geschwindigkeit bewegt sich ein Objekt auf einer Geraden, denn der Vektor der Geschwindigkeit hat für jeden Zeitpunkt der Bewegung denselben Wert: Er hat denselben Betrag und er hat dieselbe Richtung.
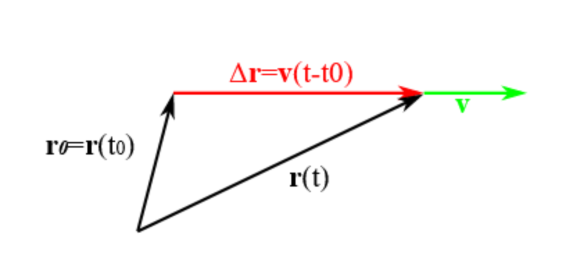
Wenn sich das Objekt zum Zeitpunkt $t_0$ an einem Punkt mit dem Ortsvektor $\textbf{r}_0$ befindet, dann wird seine Bahn durch die Funktion $\textbf{r}(t)$ beschrieben:
$\textbf{r}(t) = \textbf{r}_0 + \textbf{v} \cdot (t - t_0)$
5.7 Operationen mit Vektoren
In der Vorlesung werden Sie außer der Addition und Subtraktion von Vektoren auch das Kreuzprodukt und das Skalarprodukt von Vektoren kennenlernen. Beide spielen in der Physik eine große Rolle.
Das Kreuzprodukt verknüpft zwei Vektoren multiplikativ zu einem neuen Vektor. Wichtige physikalische Größen in der Mechanik und in der Elektrodynamik sind Kreuzprodukte.
Das Skalarprodukt ist eine Operation, die zwei Vektoren so verknüpft, dass eine ungerichtete Größe (ein Skalar) entsteht. Es ermöglicht u. a. eine kompakte Definition der Größen Arbeit und Leistung.
Mehr über diese Vektor-Verknüpfungen finden Sie in der Formelsammlung.