5. Kinematik
5.1 Koordinaten
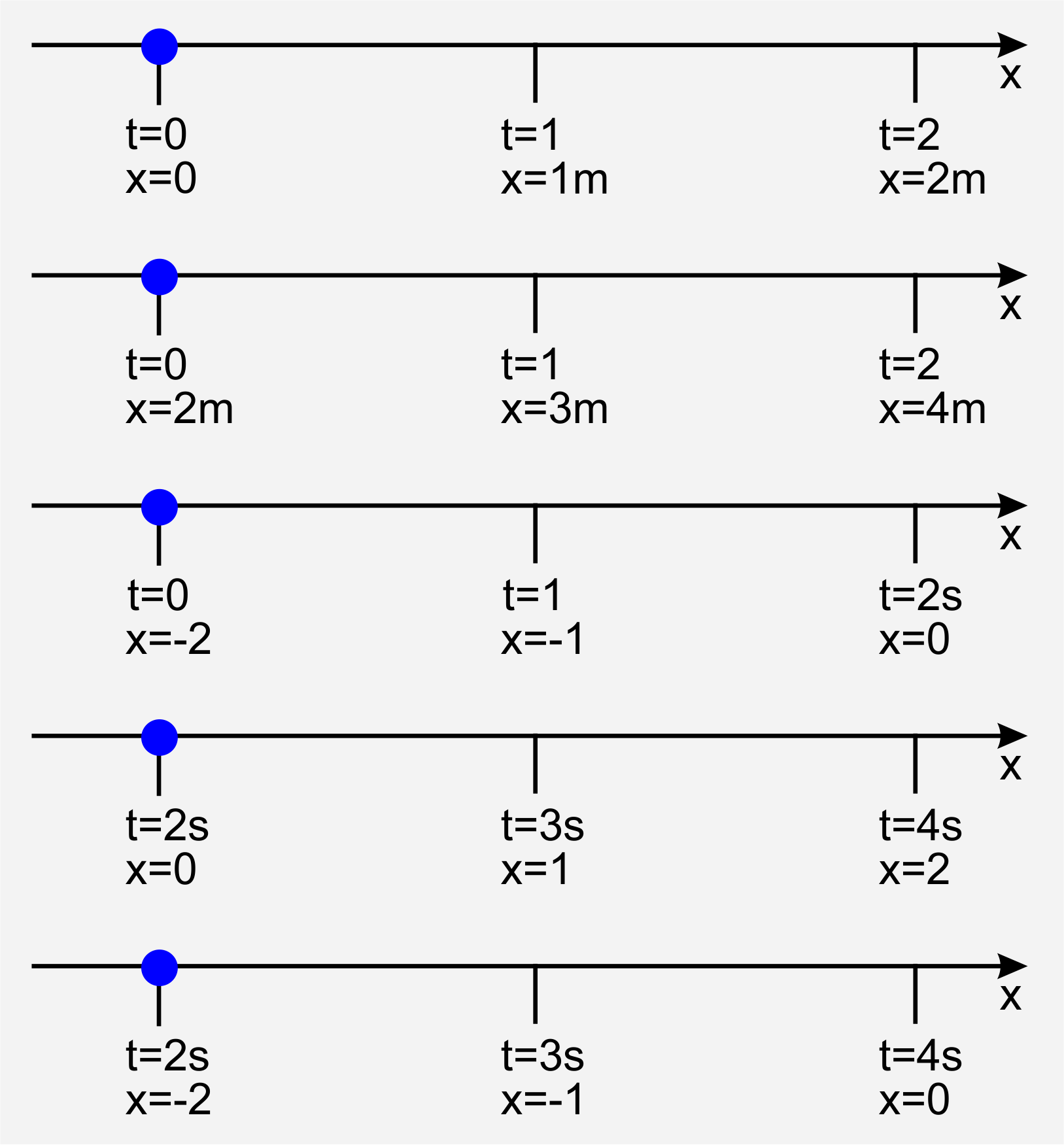
Ein Punkt bewegt sich mit konstanter Geschwindigkeit von links nach rechts längs einer Geraden. Hier sind fünf Möglichkeiten gezeigt, dieselbe Bewegung zu beschreiben:
- Bestimmen Sie jeweils die Geschwindigkeit v des Punktes.
- Wo befindet sich der Punkt jeweils zum Zeitpunkt t = 4s?
- Schreiben Sie jeweils die allgemeine Beziehung für x(t), und zeichnen Sie für jeden einzelnen Fall ein x(t)-Diagramm.
Infos:
In einem Koordinatensystem werden Punkte und Bewegungen im Raum quantitativ beschrieben. Wenn eine Bewegung längs einer Geraden verläuft, genügt zur Beschreibung meist eine einzige Koordinatenachse. Punkte im Raum können durch Ortsvektoren charakterisiert werden. Die mathematische Darstellung eines Ortsvektors ist eng mit den Koordinaten des zugehörigen Punktes verknüpft. In der Formelsammlung sind verschiedene Koordinatensysteme dargestellt.
Allgemein ist in allen Fällen: $v = \frac{\Delta s}{\Delta t} = 1ms$ und $x(t) = x_0 + v \cdot (t-t_0)$. Die einzelnen Fälle unterscheiden sich nur in der Wahl von $x_0$ und $t_0$: a) $x=4m$, b) $x=6m$ c) $x=2m$, d) $ x = 2m $, e) $ x=0$
5.2 Geschwindigkeitsvektor
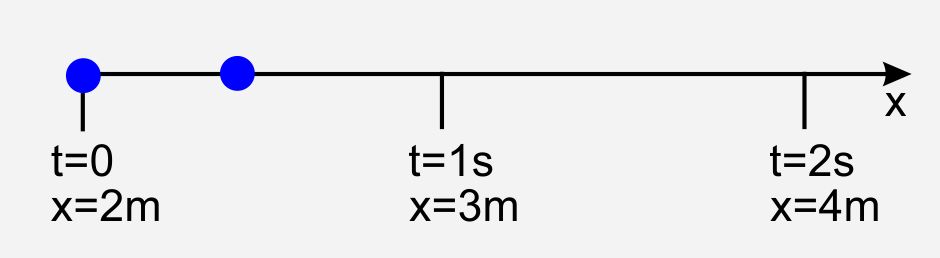
Ein Punkt bewegt sich mit konstanter Geschwindigkeit. Sie haben eine x-Achse in Bewegungsrichtung eingeführt und beobachten den Punkt zu den angegebenen Zeiten bei den angegebenen Koordinaten.
- Bestimmen Sie den Betrag der Geschwindigkeit v des Punkts.
- Bestimmen Sie den Geschwindigkeitsvektor und zeichnen Sie ihn ein.
- Was ändert sich, wenn Sie dieselbe Bewegung beschreiben wollen, die x-Achse aber von rechts nach links verläuft?
Der Betrag (Länge des Pfeils) der Geschwindigkeit ist: |v| $= 1 \frac{m}{s} $. Der Geschwindigkeitsvektor v liegt auf der x-Achse und zeigt in Richtung der Bewegung.
5.3 Sturm
Ein Flugzeug fliegt von Frankfurt nach München und zurück. Bei Windstille beträgt seine Geschwindigkeit 600km/h. Die Strecke zwischen Frankfurt und München ist 600km lang. Das Flugzeug ist also 2 Stunden unterwegs. (Schaubild: Amargeddon6 - Own work, CC BY-SA 3.0, Link)
- Wie lange dauert der Flug unter sonst gleichen Bedingungen, wenn ein Sturm mit 100km/h Windgeschwindigkeit aus südlicher Richtung weht?
- Wie gross ist die Geschwindigkeit über Grund auf dem Hin- und Rückweg?

Hinflug: $500 \frac{km}{h}$, Rückflug: $700 \frac{km}{h}$. Das Flugzeug ist für Hin- und Rückflug zusammen zwei Stunden unterwegs (123min).
5.4 Fahrplan
Auf einer zweigleisigen Strecke fahren zwei Züge mit jeweils konstanter Geschwindigkeit aufeinander zu. Der eine Zug fährt um 12.05 Uhr mit $81 \frac{km}{h}$ durch den Bahnhof von Alsbach in Richtung Bensheim, der andere Zug fährt um 12.08 Uhr mit $27 \frac{km}{h}$ durch den Bahnhof von Bensheim in Richtung Alsbach. Die Schienenstrecke zwischen den Bahnhöfen in Bensheim und Alsbach ist $14,85km$ lang.
- Wann und wo treffen sich die beiden Züge?
Info:
Die Züge treffen sich, wenn sie sich zum selben Zeitpunkt am selben Ort befinden. Beschreiben Sie die Bewegung der beiden Züge mit derselben Koordinatenachse und mit derselben Zeitskala.

Die Züge treffen sich um 12.14 Uhr in $2,7km$ Entfernung von Bensheim.
5.5 Überholen
Sie fahren mit Ihrem PKW mit $130 \frac{km}{h}$ auf der Autobahn und möchten einen LKW überholen, der mit $70 \frac{km}{h}$ fährt. Ihr PKW ist 4m, der LKW 20m lang. Sie beginnen den Überholvorgang um 13.54 Uhr.
- Wann ist der Überholvorgang beendet?
- Welche Strecke haben Sie dabei zurückgelegt?
- Betrachten Sie den Vorgang einmal von der Straße aus und einmal vom LKW aus.
Infos:
Welche Strecke muss der PKW in Bezug auf den LKW aufholen? Mit welcher Geschwindigkeit bewegt er sich relativ zum LKW? Berechnen Sie zuerst die Zeit, die für den Überholvorgang erforderlich ist.

Der Überholvorgang dauert 1,44s. Der PKW legt dabei auf der Straße 52m zurück, relativ zum LKW aber nur 24m.
5.6 Bootsfahrt
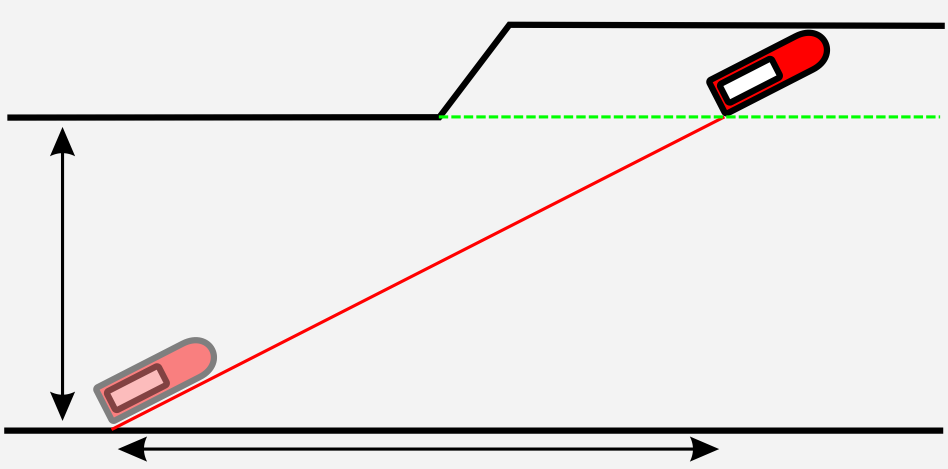
Ein Boot überquert auf einer geraden Bahn einen 30m breiten Kanal innerhalb von 120s. Parallel zur Uferlinie legt es dabei 60m zurück.
- Berechnen Sie die Geschwindigkeit des Boots, und zeichnen Sie den Geschwindigkeitsvektor ein.
Info:
Berechnen Sie die Strecke, die das Boot zurücklegt. Innerhalb welcher Zeit durchfährt es diese Strecke?
Der Betrag der Geschwindigkeit ist $0,559 \frac{m}{s}$. Der Geschwindigkeitsvektor liegt auf der Bahn des Bootes und zeigt in Richtung der Bewegung.
5.7 Strömung
Ein 20m breiter Fluss strömt gleichmässig mit einer Geschwindigkeit von 2m/s. Ein Schwimmer, der in stehendem Wasser eine Geschwindigkeit von 1m/s erreicht, schwimmt so durch den Fluss, dass seine Körperachse stets senkrecht zur Strömung ausgerichtet ist.
- Welche Strecke legt er auf dem Weg zum gegenüberliegenden Ufer zurück?
- Welche Zeit benötigt er dafür?
- Wie muss er seine Körperachse orientieren, damit er an einem Punkt ankommt, der seinem Ausgangspunkt genau gegenüber liegt?
Infos:
Die Bewegung durch die Strömung und die Bewegung des Schwimmers aus eigener Kraft relativ zum Wasser überlagern sich ungestört. Wie lange dauert die Überquerung ohne Strömung? Wie lange mit Strömung?
Der Schwimmer benötigt 20s für die Überquerung und legt dabei 44,7m zurück. Senkrecht kann er den Fluss nur durchschwimmen, wenn seine Eigengeschwindigkeit größer als $2 \frac ms$ ist.
5.8 Weitsprung
Ein sehr guter Sprinter versucht sich im Weitsprung, indem er am Absprungbalken einfach die Beine anzieht.
- Welche Sprungweite erreicht der 'Weitspringer'?
Nehmen Sie an, dass die Geschwindigkeit beim Absprung $12 \frac ms$ beträgt und der Sprinter die Beine um $ 90cm$ einfahren kann. Überlegen Sie zuerst, wie lange der Sprung dauert.
Die Sprungweite beträgt $5,14m$.