2. Auftrieb
2.1 Eisbären
Eine Eisscholle mit einer Fläche von 15m2 und einer Dicke von 40cm schwimmt im Wasser.
- Wie hoch ragt die Eisscholle aus dem Wasser?
- Wieviele Eisbären (ein Polarbär hat eine Masse von ca. 800kg) können auf der Eischolle stehen, ohne nasse Tatzen zu bekommen?
Infos:
Dichte von Eis: 0,9g/cm3 und Dichte von Seewasser: 1,02g/cm3
Die mittlere Dichte eines Körpers ist der Quotient aus seiner Masse und seinem Volumen:
ρ = m/V, die SI-EInheit ist [ρ ]= kg/m3.
Die Eisscholle taucht 35,5cm tief ein. Die maximale Zusatzlast beträgt 719kg. Schon bei einem ausgewachsenen Bären sinkt die Eisscholle!
2.2 Fahrwassertonne
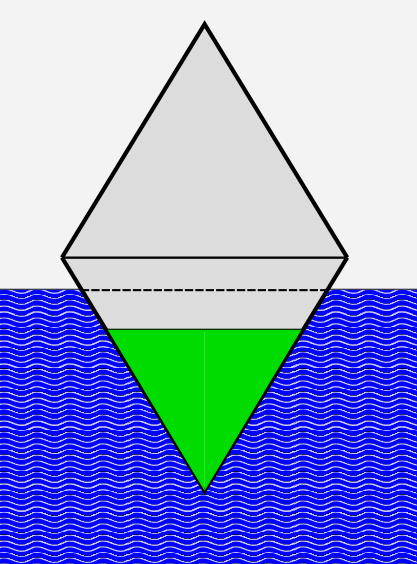
Eine Fahrwassertonne hat leer eine Masse von mT = 100kg. Sie soll h = 70cm tief ins Wasser eintauchen und wird dazu teilweise mit Sand gefüllt. Die Tonne hat die Form eines Doppelkegels mit insgesamt 1,6m Höhe und einen Durchmesser von D = 90cm. Rechnen Sie für Wasser mit der Dichte 1g/cm3.
- Welche Masse mS muss die Sandfüllung haben?
Sie müssen 13,6kg Sand einfüllen.
2.3 Sendung mit der Maus
- In der Sendung mit der Maus wurde gezeigt, dass ein Mensch abhebt, wenn man genügend viele mit Helium gefüllte Ballons an ihm befestigt. Wie viele?
Infos:
Die Hülle eines Heliumballons hat mit Befestigungsschnur eine Masse von 10g. Jeden Ballon kann man mit 20l Helium bei einer Dichte von 0,15g/l füllen. Die Dichte von Luft beträgt 1,2kg/m3. Nehmen Sie an, dass der Testpilot (Auftrieb des Testpiloten nicht vergessen) eine Masse von 75kg hat, seine Dichte soll 1g/cm3 betragen.
Mindestens 6810 Ballons sind erforderlich.