3. Ohmsches Gesetz
3.1 Parallelschaltung
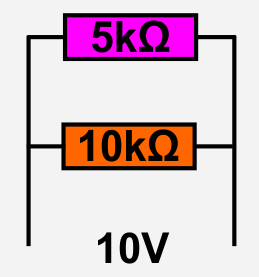
Ein Widerstand mit 5kΩ und ein Widerstand mit 10kΩ werden parallel geschaltet.
An beiden liegt eine Spannung von 10V an.
- Welcher Gesamtstrom fließt?
Es fließt ein Gesamtstrom von 3mA.
3.2 Reihenschaltung
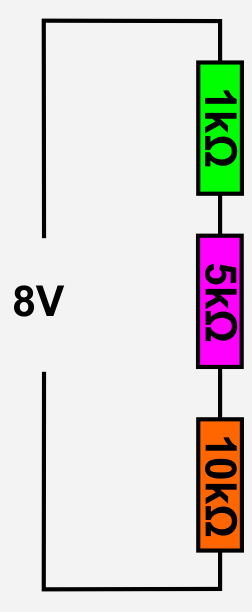
Drei Widerstände mit je 1kΩ, 5kΩ und 10kΩ werden in Reihe geschaltet.
- Welche Spannung fällt an jedem der Widerstände ab, wenn an allen dreien zusammen eine Spannung von 8V anliegt?
Info:
Der Spannungsabfall über einen Widerstand ist die Spannung, die man zwischen den Enden eines Widerstandes messen kann, wenn er von einem Strom durchflossen wird.
Die Spannungen an den Widerständen betragen jeweils 0,5V, 2,5V und 5,0V.
3.3 Netzwerk 1
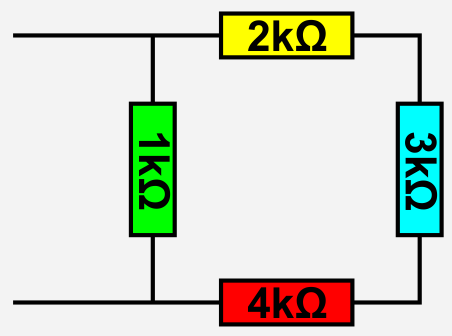
- Berechnen Sie den Gesamtwiderstand des skizzierten Netzwerks.
Info:
Der Gesamtwiderstand oder Ersatzwiderstand eines Netzwerkes ist der Widerstand, den Sie einer Schachtel zuweisen würden, in der sich das Netzwerk befindet: Sie messen den Strom, der insgesamt fließt, und die Spannung zwischen den Enden des Netzwerkes, und behandeln das Netzwerk wie einen einzigen Widerstand. Sie können den Gesamtwiderstand berechnen, indem Sie das Netzwerk in Gruppen von parallelen und in Reihe geschalteten Widerständen zerlegen.
Der Gesamtwiderstand des Netzwerks beträgt 0,9kΩ.
3.4 Netzwerk 2
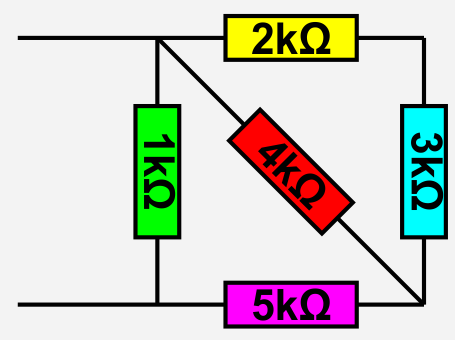
- Berechnen Sie den Gesamtwiderstand des skizzierten Netzwerks.
Info:
Zeichnen Sie die Schaltung so um, dass alle Widerstände 'senkrecht' ausgerichtet sind! Welche Widerstände sind parallel, welche in Reihe?
Der Gesamtwiderstand des Netzwerks beträgt 0,878kΩ.
3.5 Netzwerk 3
- Berechnen Sie den Gesamtwiderstand des skizzierten Netzwerks.

Der Gesamtwiderstand des Netzwerks beträgt 1,47kΩ.
3.6 Kombination
Sie möchten einen Widerstand von 1kΩ ± 0,1% realisieren, haben aber nur einen Widerstand von 1,013kΩ. Sie kommen auf die Idee, diesen Widerstand mit einem zweiten Widerstand Rx so zu kombinieren*, dass sich der gewünschte Gesamtwiderstand ergibt.
- Welchen Wert darf Rx dafür maximal, welchen Wert darf er minimal haben?
Info:
Müssen Sie einen Widerstand parallel oder in Reihe schalten? Welche Maximal- und Minimalwerte darf der Gesamtwiderstand annehmen?
Sie müssen den Widerstand parallel schalten. Er muss zwischen 72,3kΩ und 84,5kΩ liegen.