1. Physikalische Größen
1.1 NASA-Crawler
Der "NASA-Crawler" legt in einer Stunde eine Strecke von einer Meile (1Meile = 1,609km) zurück, das Licht durchläuft in 1 ns eine Strecke von 30cm, ein Baum wächst mit einer Geschwindigkeit von 4m in 3 Jahren.
Geben Sie die jeweiligen Geschwindigkeiten in der SI-Einheit $\frac{m}{s}$ an.
Tabelle der SI-Basiseinheiten
SI-Basiseinheiten im Atlas
(Foto: NASA - Public Domain, wikimedia)
Crawler: $v=0,447 \frac{m}{s}$, Licht: $c=3 \cdot 10^8 \frac{m}{s}$, Baum: $v=4,2 \cdot10^{-8} \frac{m}{s}$
Die (mittlere) Geschwindigkeit ist definiert als zurückgelegte Strecke innerhalb der zugehörigen Zeit:
$$v=\frac{\Delta s}{\Delta t}\text{ , also:}$$
Crawler:
$$v=\frac{\Delta s}{\Delta t}=\frac{1,609 km}{60 min}=\frac{1.609 m}{60 \cdot 60 s} = 0,447 \frac{m}{s}$$
Licht:
$$v=\frac{\Delta s}{\Delta t}=\frac{30 cm}{1 ns}=\frac{0,3 m}{1 \cdot 10^{-9} s} = 0,3 \cdot 10^{9} \frac{m}{s} = 0,3 \cdot 10^{8} \frac{m}{s}$$
Baum:
$$v=\frac{\Delta s}{\Delta t}=\frac{4 m}{3 \cdot 365 \cdot 24 \cdot 60 \cdot 60 s}=4,2 \cdot 10^{-8}\frac{m}{s} = 42 \frac{nm}{s}$$
1.2 Marmorsäule
Berechnen Sie die Masse einer Marmorsäule (Tipp: die Säule ist in guter Näherung ein Zylinder). Der Durchmesser beträgt 1m, die Höhe 10m, die Dichte 2,5g/cm3. Die mittlere Dichte eines Körpers ist der Quotient aus seiner Masse und seinem Volumen: ρ = m/V, die SI-EInheit ist [ρ ]= kg/m3.
Die Masse der Säule beträgt $m=19,6 \cdot 10^3 kg$.
Die Säule ist in guter Näherung ein Zylinder mit dem Durchmesser d und der Höhe h.
Ihr Volumen V ist das Produkt aus Grundfläche und Höhe:
$V=A \cdot h = \pi \cdot \frac{d^2}{4} \cdot h$
Ihre Masse ist:
$m=\rho \cdot V =\rho \cdot \pi \cdot \frac{d^2}{4} \cdot h $
$m = 2,5 \cdot 10^3 \frac{kg}{m^3} \cdot \pi \cdot \frac{(1 m)^2}{4} \cdot 10 m = 19,6 \cdot 10^3 kg$
Die Masse der Marmorsäule beträgt etwa 20t. Überrascht?
1.3 Erde
Die mittlere Entfernung der Erde von der Sonne beträgt 150 Millionen Kilometer. Berechnen Sie die Geschwindigkeit der Erde auf ihrer Bahn um die Sonne. Die Erdbahn ist in guter Näherung eine Kreisbahn.
Die Bahngeschwindigkeit der Erde beträgt $v = 3,0 \cdot 10^4 \frac{m}{s}$.
Die Umlaufzeit T der Erde für eine komplette Kreisbahn mit Umfang U um die Sonne beträgt ein Jahr. Der Radius der Kreisbahn ist angegeben.
Die Bahngeschwindigkeit der Erde beträgt also:
$v = \frac{U}{T} = \frac {2\pi \cdot r}{T}$
$v=\frac {2\pi \cdot 1,5 \cdot 10^{11} m^3}{3,1536 \cdot 10^7 s} = 3,0 \cdot 10^4 \frac{m}{s}$
1.4 Fichte
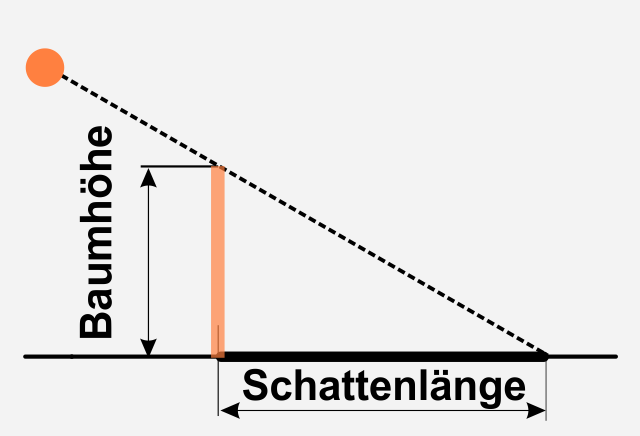
Sie möchten die Höhe einer Fichte bestimmen. Dazu messen Sie die Länge des Schattens, den der Baum am Nachmittag wirft. Der Schatten ist 30m lang, wenn die Sonne 30° über dem Horizont steht.
Wie hoch ist die Fichte?
Die Fichte ist $h = 17,3 m$ hoch.
Da es sich um ein rechtwinkliges Dreieck handelt, gilt folgende Beziehung:
$\tan \alpha = \frac{\text{Baumhöhe h}}{\text{Schattenlänge l}}$
Damit berechnet sich die Baumhöhe zu:
$h = l \cdot \tan \alpha = 30 m \cdot \tan {30°} = 17.3 m$
Die Fichte ist also etwa 17m hoch.
1.5 Kompasstauchen
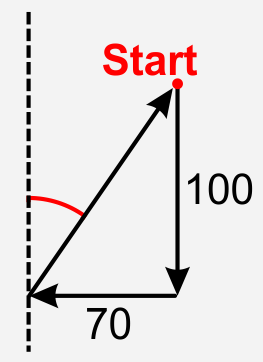
Ein Taucher möchte einen Dreieckskurs tauchen, der ihn zu seinem Ausgangspunkt zurückbringt. Er zählt 100 Flossenschläge auf Kurs 180° genau nach Süden, dann 70 Flossenschläge auf Kurs 270° genau nach Westen.
Unter welchem Kompasskurs kommt er zu seinem Ausgangspunkt zurück?
Wie viele Flossenschläge sind es bis dahin?
Der Kurswinkel ist $\alpha = 35°$, nach 122 Flossenschlägen ist der Ausgangspunkt wieder erreicht.
Die drei Strecken bilden ein rechtwinkliges Dreieck. Der gesuchte Kurswinkel tritt innerhalb dieses Dreiecks nochmals auf. Für diesen Winkel gilt:
$\tan \alpha = \frac{b}{a} \qquad \Rightarrow \qquad \alpha = \arctan {\frac{b}{a}} = \arctan {0,7} = 35°$
Die Länge der Seite c finden Sie z. B. aus:
$\sin \alpha = \frac{b}{c} \qquad \Rightarrow \qquad c = \frac{b}{\sin \alpha} = \frac{70}{\sin{35°}} = 122$
1.6 Daumenmaß
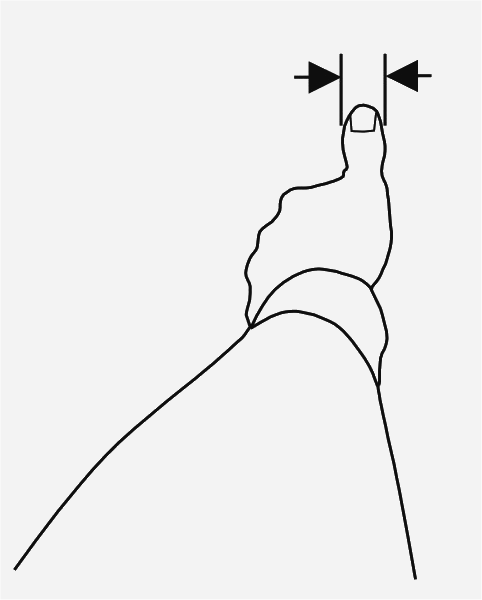
Jeder von Ihnen trägt einen Winkelmesser mit sich herum: den Daumen. Strecken Sie Ihren Arm aus, und visieren Sie Ihren nach oben gereckten Daumen an.
Welchen Winkel überdecken Sie damit?
Geben Sie das Ergebnis im Grad- und Bogenmaß an.
Realistische Angaben (vergleichen Sie mit Ihren individuellen Werten):
Abstand Auge zum Daumen: 65cm
Daumendicke: 23mm
(Skizze: Schorschi2 aus der deutschsprachigen Wikipedia, CC BY-SA 3.0, Link)
Der Winkel beträgt $\beta = 0,03538 rad = 35,4 mrad$, das sind 2,03°.
Sie können hier den Winkel direkt im Bogenmaß berechnen. Bei so kleinen Winkeln ist die Sekante (der Daumendurchmesser D) in sehr guter Näherung genauso lang wie der Kreisbogen. Die Armlänge L ist der Radius des Kreises.
Sie können also direkt die Definition des ebenen Winkels im Bogenmaß benutzen:
$\beta_{rad} = \frac{D}{L} = \frac{23mm}{650mm}=0,03538rad$
$\beta_{Grad} =\frac{180°}{ \pi} \cdot \beta_{rad}$
$\beta_{Grad} =\frac{180°}{ \pi} \cdot 0,0354 = 2,03°$
1.7 Numerische Apertur
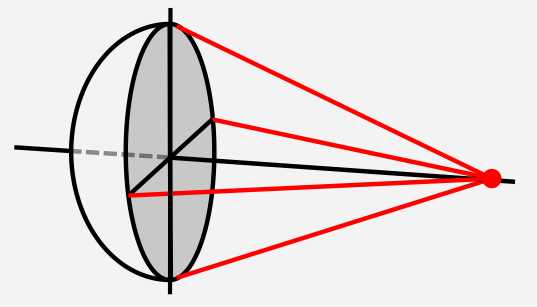
Berechnen Sie für eine Linse mit einem Durchmesser von 45mm und einer Schnittweite (Abstand zwischen Fokus und Linsenoberfläche) von 25mm den halben Öffnungswinkel des Akzeptanzkegels, das ist der Lichtkegel, der von einer punktförmigen Lichtquelle im Fokus ausgeht und von den Strahlen begrenzt wird, die auf die Ränder der Linse fallen..
Der halbe Öffnungswinkel beträg $\alpha = 42°$.
$\tan \alpha = \frac{D/2}{S} \qquad \Rightarrow \qquad \alpha = \arctan \left( \frac{D/2}{S} \right)$
$\alpha = \arctan \left( \frac{45mm/2}{25mm} \right) = 41,987° \approx 42°$
Die numerische Apertur ist das Produkt aus dem Brechungsindex des umgebenden Mediums und dem Sinus dieses Winkels. Mehr darüber in der Optikvorlesung!